| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 윈도우
- 윈도우프로그래밍
- Win32 API
- 컴퓨터 구조
- OpenGL
- 핵심 API로 배우는 윈도우프로그래밍
- MFC 윈도우 프로그래밍
- win32
- 윈도우 프로그래밍
- 윈도우 구조
- 렌더링
- Graphics
- denoising
- 컴퓨터 아키텍쳐
- 셰이더프로그래밍
- 그래픽스
- 오픈지엘
- 운영체제
- window programming
- shader programming
- MFC
- bezier curve
- modeling
- c4d
- Mesh Processing
- 셰이더
- 그래픽스기초
- shader
- Geometry Modeling
- 베지에 곡선
- Today
- Total
오다기리 박의 알고리즘 노트
회전운동 본문
각속도(Angular Velocity)
회전운동에서 가장 기본적이면서 중요한 개념은 각속도(angular velocity)이다.

각속도는 말 그대로 각도가 시간에 따라 어떻게 변하는가를 나타내는 양이다. 그림에서 보듯이 반지름이 r인 원 위에 물체 P가 있을 때 각도 θ에 대한 호의 길이는 l이며

의 관계가 있다. 양변을 시간에 대해 미분하면

의 관계가 성립함을 알 수 있다. 여기서 v는 선속도, ω는 각속도를 나타낸다. 속도와 각속도의 관계만 유념하면 회전운동에 쉽게 적응할 수 있다.
회전관성(Moment of inertia)
회전운동에서 또 하나 중요한 개념으로 회전관성이라는 물리량이 있다. 회전관성과 회전운동에 대해서 알아보기 위해 다음과 같은 강체가 축을 중심으로 회전하고 있는 상황을 생각해보자. 강체(rigid body)란 여러 입자들이 모여 이루어진 물체로서 각 입자들의 상대적인 위치가 절대로 변하지 않는 물체를 일컫는다. 강체는 이상적인 개념으로서 절대적인 강체란 존재할 수 없다. 대신 우리가 상식적으로 단단하다고 인식하는 물체는 대략 근사적으로 강체라고 볼 수 있다.

이제 이 강체가 N개의 입자들로 구성되었다고 가정하고 이 강체가 그림처럼 어떤 축 주변으로 회전한다고 생각해보자. 이때의 운동에너지 K는
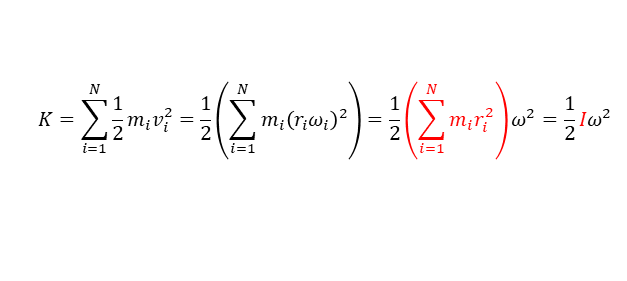
이다. 강체를 이루는 각 입자의 축에 대한 각속도 ω는 모두 같다. 여기서
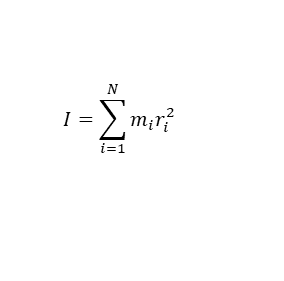
로 정의된 이 양이 바로 회전관성이다. 각 입자의 질량과 회전반지름제곱을 곱한 값을 모두 더한 값이다. 위 운동에너지 식 K를 우리가 잘 알고 있는 운동에너지의 식 1/2Mv2과 비교해보면 각속도 ω는 선속도 v에 대응되고 회전관성 I는 물체의 질량 M에 대응된다는 사실을 알 수 있다. 즉, 회전관성이란 회전하는 강체의 물리량에서 질량 역할을 하는 셈이다. I에 각 입자의 질량 m이 들어가 있는 것은 이 때문이다.
그런데 회전반지름제곱 ri2이 회전관성에 들어가 있는 점에 유의할 필요가 있다. 우리는 경험적으로 회전축에서 멀리 떨어져 있을수록 잘 돌아간다는 것을 알고 있다. 그 효과가 ri2에 들어가 있는 셈이다.
질량이 연속적으로 분포된 경우를 보자.
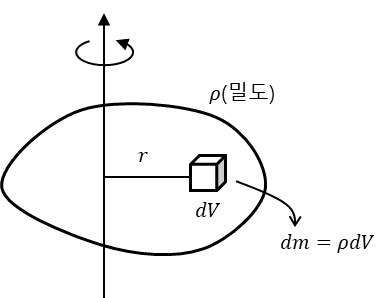
여기서 dm은 강체를 이루는 부피요소의 질량으로, 밀도를 도입해서 dm = ρdV 로 쓸 수 있다. 그러면 회전 관성은
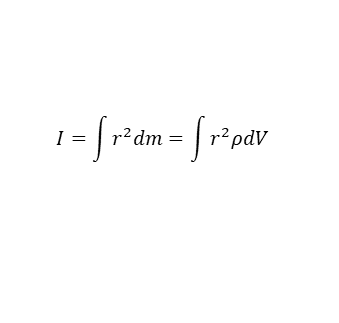
이다. 회전관성은 같은 강체라고 하더라도 회전축이 어디냐에 따라 달라진다. 왜냐하면 축의 위치에 따라 각 구성입자들의 회전반지름이 달라지기 때문이다.
예를 들어 구의 중심을 지나는 축으로 회전하는 구의 회전관성을 구해보자.
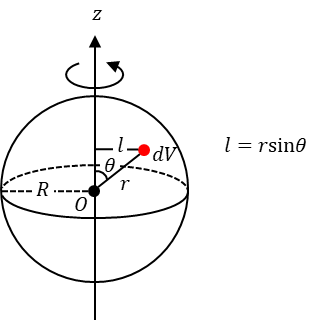
구의 회전관성 I는 다음과 같다.
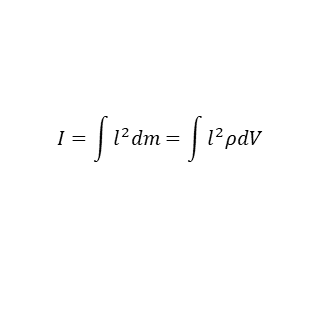
구의 회전관성은 당연히 구면좌표계에서 계산하는 것이 편리하다. 구면좌표계에서 구의 부피요소는 dV = r2sinθ⋅dr⋅dθ⋅dφ이므로 I는 다음과 같이 다시 쓸 수 있다.
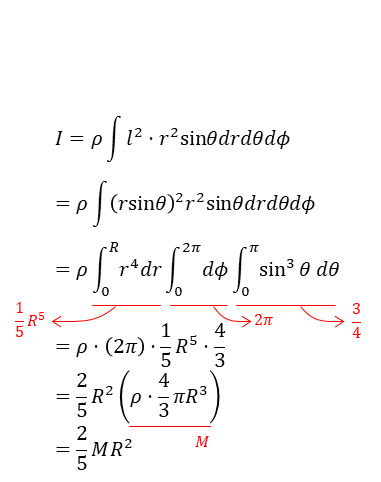
구의 회전관성은 결론적으로 말해서 I = 2/5MR2이다. 이 말은 반지름이 R인 구를 그 중심축으로 회전시킬 때의 회전효과는, 구의 질량의 40%에 해당하는 질량(2/5M)을 R만큼 떨어진 곳에 위치시켰을 때의 회전효과와 같다는 것이다. 왜 이렇게 차이가 날까? 그것은구라는 물체를 구성하는 구성입자들이 회전축에서 떨어져 있는 위치가 다 다르기 대문이다. 구는 직관적으로 생각해봤을 때 비교적 축 주위에 구의 많은 질량이 분포해 있다는 것을 알 수 있다. 축에 가까운 입자들은 회전관성이 줄어든다. 따라서 모든 질량이 R만큼 떨어져 있을 때보다 회전관성은 작아질 것이다. 그 효과가 40%라는 얘기다.
속이 꽉 찬 구 대신에 모든 질량이 껍데기에만 분포하는 공껍질의 회전관성은 어떨까? 모든 질량이 R만큼 떨어진 공의 표면에만 존재하므로 구의 경우보다 회전축에서 멀게 질량들이 분포해 있는 셈이다. 따라서 같은 질량이고 같은 반지름이라면 공껍질의 회전관성이 구의 회전관성보다 더 크다는 것을 직관적으로 알 수 있다. 실제 계산을 해보면 I = 2/3MR2이다.
평행축 정리(Parallel-Axis Theorem)
평행축 정리란 강체를 회전시킬 때 회전축을 평행하게 이동한 효과가 강체의 회전관성에 어떤 영향을 주는가에 대한 정리이다. 위에서 말해했듯이 회전관성은 어떤 축을 중심으로 강체를 회전시키느냐에 따라 달라진다. 축이 주어질 때마다 각 입자의 질량과 회전반지름제곱을 곱한 값을 모두 더하는 공식으로 회전관성을 구한다면 아주 귀찮을 것이다. 평행축 정리를 이용하면 이 수고를 획기적으로 줄여준다.

위 그림에서 1번 축이 강체의 질량중심을 지나고 2번 축이 그와 평행하게 L만큼 떨어져 있다. 1번 축을 중심으로 한 회전관성은 Icom, 2번 축을 중심으로 한 회전관성을 I라고 했을 때 이 둘 사이에는 I = Icom + ML2의 관계가 성립한다. 이 정리에 따르면 임의의 축을 중심으로 한 회전관성 I는 그 축에 평행하고 질량중심을 지나는 축을 중심으로 한 회전관성 Icom만 알면 쉽게 구할 수 있다.
돌림힘 (torque)
돌림힘은 회전운동에서 힘에 대응되는 물리량이다. 예를 들어 문을 열 때 똑같은 힘을 주더라도 그 힘이 문의 회전축에서 얼마나 멀리 떨어져 있느냐에 따라 문을 더 쉽게 열 수도 더 어렵게 열 수도 있다. 따라서 돌림힘에는 회전반지름이 어떻게된 개입돼 있다. 실제로 돌림힘 τ는 다음과 같이 정의된다.
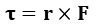
여기서 F는 힘 벡터, r은 힘이 작용하는 점의 변위이다. 이 두 벡터가 벡터곱으로 곱해져서 돌림힘을 정의한다. 두 벡터가 평행하면 돌림힘은 0벡터이다.
돌림힘은 회전운동에서 힘의 역할을 하는 물리량으로서 F = ma에 대응되는 회전운동의 방정식은 τ = Iα이다. 여기서 I는 회전관성으로서 회전운동의 질량에 해당하는 양이고 α는 각가속도이다.
회전운동에너지 (Rational Kinetic Energy)
굴러가는 바퀴의 회전운동에너지를 구해보자. 바퀴를 구성하는 모든 입자의 운동에너지를 다 더하면 앞서 보았듯이 바퀴라는 강체의 운동에너지는
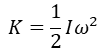
으로 주어진다. 여기서 I는 회전관성인데, 아래 그림처럼 바퀴가 미끄러지지 않고 지면에 계속 맞닿아 오른쪽으로 굴러가면 바퀴는 지면과 닿는 점 O를 중심으로 회전하는 것과도 같다.

따라서 평행축 정리에 의해 I = Icom + Mr2이고 바퀴의 운동에너지는
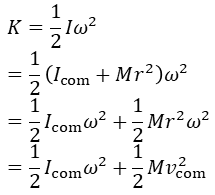
이다. 식의 첫째 항은 바퀴가 질량중심을 지나는 축을 중심으로 회전할 때의 회전운동에너지이고 둘째 항은 질량 중심이 속도 vcom으로 선운동할 때의 운동에너지이다.
따라서
(굴러가는 바퀴의 운동에너지) = (질량중심을 지나는 축으로 회전하는 회전운동에너지) + (질량중심이 직선으로 운동하는 에너지)
이다.
그러니까, 강체에 똑같은 에너지를 주었을 때 강체의 회전운동에너지가 커지면 그만큼 질량중심이 날아가는 속도는 줄어든다. 위 식은 꼭 바퀴가 아니더라도 회전하는 물체에 일반적으로 적용된다.
각운동량 (Angular Momentum)
각운동량은 회전운동에서 가장 중요한 개념 중 하나라고 볼 수 있다. 각운동량은 직선운동에서의 운동량에 대응하는 개념으로서 다음과 같이 정의된다.
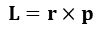
여기서 r은 힘이 작용하는 점의 변위, p는 선운동량이다. 이 두 벡터가 벡터곱으로 곱해져서 각운동량을 정의한다.
r과 p가 수직이라고 가정하면 p= mv에 대응되는 각운동량의 방정식은 L = Iω이다. 여기서 I는 회전관성으로서 회전운동의 질량에 해당하는 양이고 ω는 각속도이다.
선운동에서 운동량의 보존이 중요하듯이 회전운동에서도 각운동량보존이 중요하다. 각운동량의 보존 또한 외부의 돌림힘이 작용하지 않을 때 성립하는 보존법칙이다.
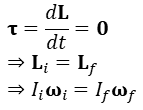
즉, 외부 돌림힘이 없으면 각운동량의 값은 언제나 똑같다. i는 초기값, f는 나중값을 나타낸다. 예를 들어 의자에 앉아 몸을 시계방향으로 돌리려면 땅바닥을 반시계 방향으로 밀어 돌려야 한다. 이는 로켓이 앞으로 나아가기 위해 연료를 뒤로 분사해야하는 것과 근본적으로 같은 이치이다.
[참고] 이종필. 『이종필의 아주 특별한 상대성이론 강의』. 동아시아, 2015.
'물리학' 카테고리의 다른 글
| 측량텐서 (0) | 2024.01.24 |
|---|---|
| 상대성이론의 4차원 벡터에 대하여 (4) | 2024.01.09 |
| 케플러의 행성 운동 법칙(Kepler's laws of planetary motion) (1) | 2023.11.14 |
| 만유인력의 법칙(Universal Law of Gravitation) (1) | 2023.08.14 |
| 특수상대성 이론 (0) | 2023.06.06 |




