| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 베지에 곡선
- Mesh Processing
- 핵심 API로 배우는 윈도우프로그래밍
- 운영체제
- 셰이더
- 컴퓨터 아키텍쳐
- shader
- 윈도우프로그래밍
- Geometry Modeling
- MFC 윈도우 프로그래밍
- 렌더링
- window programming
- 셰이더프로그래밍
- shader programming
- 그래픽스
- 컴퓨터 구조
- denoising
- Graphics
- 윈도우 프로그래밍
- modeling
- OpenGL
- 그래픽스기초
- MFC
- 오픈지엘
- Win32 API
- 윈도우
- c4d
- bezier curve
- win32
- 윈도우 구조
- Today
- Total
오다기리 박의 알고리즘 노트
직교 좌표계(Orthogonal Coordinates), 원기둥좌표계(Cylindrical Coordinate System) , 구면과표계(Spherical Coordinates) 본문
직교 좌표계(Orthogonal Coordinates), 원기둥좌표계(Cylindrical Coordinate System) , 구면과표계(Spherical Coordinates)
오다기리 박 2022. 8. 20. 23:433차원 공간을 나타내기 위해 사용하는 몇 가지 좌표계에 대해서 알아보려고 한다. 우리에게 가장 익숙한 직교 좌표계는 직각으로 만나는 축들을 이용하여 위치를 표현한다.

다중적분을 이용하여 3차원 부피를 적분할 때 적분 요소는 dxdydz이다. 이것은 3차원 공간에서 x, y, z가 극소량으로 변화할 수 있는 범위를 표현한 것으로, 세 변이 각각 dx, dy, dz인 정육면체의 부피라고 할 수 있다. 따라서 dxdydz는 극소한 부피요소, 즉 dV라고 할 수 있다.
직교좌표계에서 공간 속의 한 점 P(x, y, z)를 각 축 방향으로 조금씩 변화시켜서 얻은 점을 Q라 하면 Q는 Q(x+dx, y+dy, z+dz)가 된다. 이 두 점 사이의 거리 ds는 피타고라스 정리에 의해 ds2 = dx2 + dy2 + dz2가 된다. 이렇게 특정한 좌표계에서 두 점 사이의 거리를 재는 방식을 '측량(metric)'이라고 한다. 뒤에서 원기둥 좌표계, 구면 좌표계에서의 측량도 알아볼 것이다. 측량은 일반상대성이론에서 가장 기본이 되는 개념이다.
이제 직교좌표계를 원기둥 좌표계로 바꿔보자. 공간 속의 한 점 P를 세 개의 변수로 정할 때, 원기둥의 모양처럼 원 모양의 극좌표와 그에 수직 한 길이 좌표를 사용한다. 직교 좌표계와 원기둥 좌표계 사이의 관계식은 다음과 같다.

(x, y, z)로 표현된 직교좌표계를 (ρ, φ, z)로 표현된 원기둥 좌표계로 바꾸는 과정은 다음과 같다.

직교 좌표계의 부피 요소는 dV = dxdydz로 주어지는 반면 원기둥 좌표계의 부피 요소는 dV = dρ(ρdφ)dz가 된다. 여기서 ρ와 φ는 xy-평면을 극좌표로 표현하는 좌표임을 알 수 있다. 또한 직교 좌표계를 원기둥 좌표계로 바꾸는 자코비안은 ρ임을 알 수 있다. (이 경우 3 X 3 행렬의 행렬식이다.)
또한 원기둥 좌표계에서의 측량은 ds2 = dρ2 + ρ2dφ2 + dz2가 된다. 원기둥 위의 두 점 사이의 거리를 잰 것이라고 할 수 있다.
이번에는 직교좌표계를 구면 좌표계로 바꿔보자. 공처럼 구면 대칭성이 있는 경우에는 구면 좌표계를 쓰는 것이 훨씬 편리하다. 직교 좌표계와 구면 좌표계 사이의 관계식은 다음과 같다.
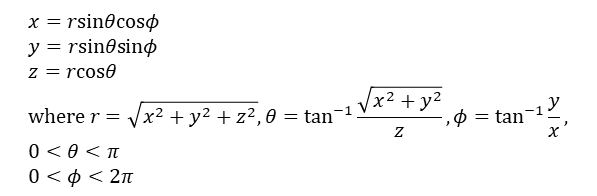
(x, y, z)로 표현된 직교좌표계를 (r, θ, φ)로 표현된 구면 좌표계로 바꾸는 과정은 다음과 같다.
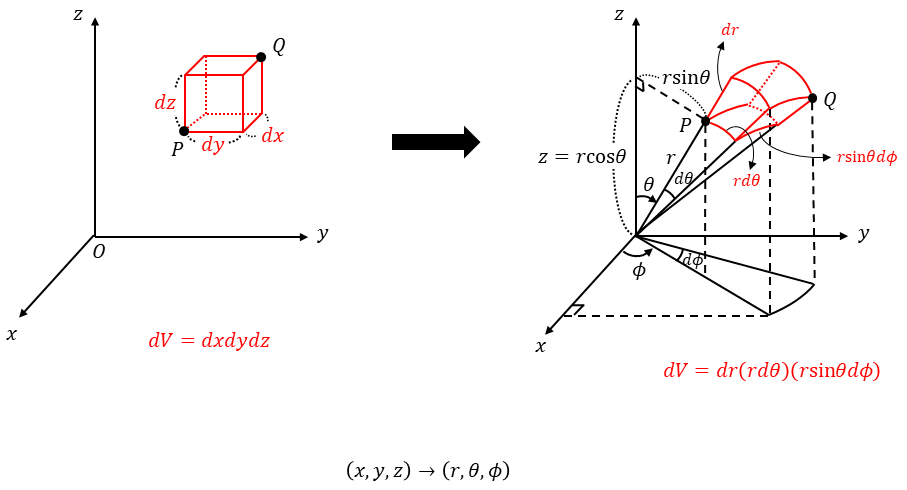
그림이 다소 복잡해 보일 수 있지만 공 위의 한 점을 수학적으로 결정하기 위해서 무엇이 필요한지를 생각해보자. 우선 원점에서 구 위의 점 P까지의 거리는 구의 반지름 r이다. 그 다음으로는 두 각도가 필요하다. 지구에서 어느 위치를 정하기 위해서 위도와 경도가 필요한 것과 똑같다. 경도 φ는 +x축 기준으로 한바퀴를 완전히 돌아 360도를 잰다. 일단 φ가 360도를 커버하면 위도는 +z 축을 기준으로 180도까지만 재면 된다. rsinθ의 값은 z축에서 얼마나 떨어져 있는지 재는 양이다.
구면 좌표계의 부피 요소는 그림에서 알 수 있듯이 dV = dr(rdθ)(rsinθdφ)가 된다. 또한 직교좌표계를 구면 좌표계로 바꾸는 자코비안은 r2sinθ임을 알 수 있다. 또한 구면 좌표계에서의 측량은 ds2 = dr2 + r2sin2θdφ2 + r2dθ2가 된다.
구면 좌표계에서의 부피 요소를 그대로 적분하면 구의 부피가 나온다.
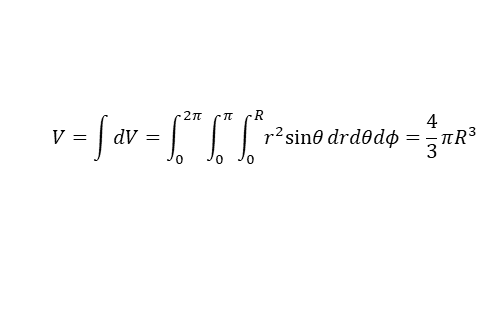
한편 구의 겉넓이는 r값이 고정된 상황이므로 두 개의 각도에 대한 적분만 진행하면 된다. r값이 고정된 상황에서의 면적 요소는 dS = rdθ(rsinθdφ)로 주어지므로 구의 겉넓이는
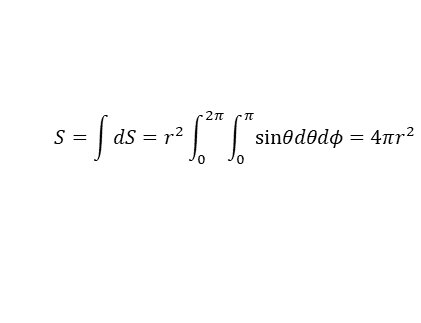
임을 알 수 있다.
[참고] 이종필. 『이종필의 아주 특별한 상대성이론 강의』. 동아시아, 2015.
'미적분학' 카테고리의 다른 글
| 매개변수 곡면 (Parametric Surface) (0) | 2022.09.21 |
|---|---|
| 선적분(Line Integral) (2) | 2022.09.20 |
| 미분연산자: 그래디언트(Gradient), 발산(Divergence), 컬(Curl), 라플라시안(Laplacian) (1) | 2022.09.05 |
| 자코비안(Jacobian) (0) | 2022.08.20 |
| 다중적분 (0) | 2022.08.12 |




