| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 윈도우 프로그래밍
- MFC
- shader
- Geometry Modeling
- c4d
- 컴퓨터 아키텍쳐
- Graphics
- 베지에 곡선
- 핵심 API로 배우는 윈도우프로그래밍
- MFC 윈도우 프로그래밍
- modeling
- 그래픽스
- 셰이더
- 컴퓨터 구조
- denoising
- 운영체제
- window programming
- 렌더링
- 오픈지엘
- win32
- bezier curve
- 윈도우프로그래밍
- Win32 API
- Mesh Processing
- shader programming
- 윈도우
- OpenGL
- 셰이더프로그래밍
- 윈도우 구조
- 그래픽스기초
- Today
- Total
오다기리 박의 알고리즘 노트
상대성이론의 4차원 벡터에 대하여 본문
3차원 공간벡터는 3개의 성분을 가지며, x, y, z 성분을 가진다.
4벡터 즉, 4차원 벡터는 4개의 성분을 가지며 3개의 공간성분(x, y, z)에 시간성분(t)이 하나 더 들어가 있다. 시간 성분이 새롭게 들어가는 이유는 상대성이론이 시간과 공간을 하나로 엮었기 때문이다.
상대성이론에서 시간과 공간이 하나로 엮여 시공간(spacetime)이 된 것은 광속 때문이다. 아인슈타인은 특수상대성이론을 만들면서 모든 관성좌표계에서 광속이 항상 일정하다는 '광속불변'을 자기 이론의 첫 번째 전제조건으로 내세웠다.
광속도 속력의 일종이므로 시간과 공간의 변수들로 정의되는 양이다. 그런데 이 값이 임의의 관성좌표계(서로 등속운동을 하는 좌표계)에서 항상 똑같은 값을 가지려면 시간과 공간이 특별하게 얽힐 수 밖에 없다. 뉴턴역학에서 시간은 시간대로 공간은 공간대로 따로따로 존재하는 물리량이었지만, 아인슈타인에 이르러서는 모든 것이 광속을 중심으로 돌아간다. 시간과 공간은 뉴턴역학에서처럼 더 이상 절대적인 지위를 갖지 못하고 불변의 광속에 종속된 물리량일 뿐이다.
이것을 좀 더 자세하게 살펴보기 위해 빛이 Δt라는 시간 동안 이동한 거리 cΔt를 생각해보자. 이 시간 동안 x, y, z 좌표가 각각 Δx, Δy, Δz만큼 변했다고 하면 피타고라스의 정리에 따라 아래와 같은 관계가 성립한다.

만약 우리가 또 다른 좌표계를 도입해서 빛의 이동거리를 기술하면 이 때는 다음과 같이 쓸 수 있다.

시간과 공간의 모든 좌표에 붙은 프라임(')은 이것이 새로운 좌표계의 좌표임을 뜻한다. 하지만 광속 c에는 프라임이 붙지 않았다. 두 식의 광속이 모두 c로 똑같다는 것이 바로 광속불변의 법칙이다. 편의상 광속을 1로 두면 (c = 1) 물체가 광속에 가까이 다가가는 현상을 묘사할 수 있다.
위 식을 4벡터의 곱으로 표현할 수 있다.

4벡터의 첫 성분은 0성분으로서 시간성분이라고도 한다. 나머지 1, 2, 3 성분은 보통의 3차원 공간벡터의 성분과 같다. 즉 4벡터란 4차원 공간벡터에 0번째 시간성분을 하나 더한 벡터이다. ΔXμ를 반변벡터(contravariant vector), ΔXμ를 공변벡터(covariant vector)라고 부른다. 그리고 시그마합을 다음과 같이 시그마 기호가 생략된 아인슈타인 표기법으로 나타낼 수도 있다.

이렇게 똑같은 첨자가 아래위로 반복되면서 더해진 형태를 첨자의 축약(contraction)이라고 부른다.
빛의 이동거리에 대한 식을 다시 써보자.
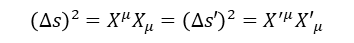
이와 같은 조합 즉 2개의 4벡터가 XμXμ의 형태로 곱해져 있으면 좌표변환에 대해서 불변(invariant)인 양이다. 우리에게 익숙한 3차원의 유클리드 공간에서는 3개의 공간성분의 제곱의 합(두 3차원 점 사이의 거리 등)이 불변량을 이룬다. 반면에 4차원 공간에서는 위 식처럼 시간성분의 제곱과 공간성분의 제곱의 차이가 불변량을 이룬다. 이와 같은 공간을 민코프스키 공간이라고 한다. 상대성이론을 직관적으로 이해하기 어려운 이유는 그 무대가 되는 민코프스키 공간이 우리의 경험에 익숙하지 않기 때문이다.
상대성이론의 핵심은 관측자의 상대적 운동에 따라서 바뀌지 않는 물리법칙이다. 어느 좌표계에서도 광속은 변하지 않으며 따라서 위 식과 같은 스칼라양도 변하지 않는다. 이처럼 상대성이론은 변하지 않는 물리적 진실이 좌표변환에 대해 불변으로 유지되게끔 다른 것들이 어떻게 바뀌는가에 대한 이론이다.
[참고] 이종필. 『이종필의 아주 특별한 상대성이론 강의』. 동아시아, 2015.
'물리학' 카테고리의 다른 글
| 측량텐서 (0) | 2024.01.24 |
|---|---|
| 케플러의 행성 운동 법칙(Kepler's laws of planetary motion) (1) | 2023.11.14 |
| 만유인력의 법칙(Universal Law of Gravitation) (1) | 2023.08.14 |
| 회전운동 (0) | 2023.08.14 |
| 특수상대성 이론 (0) | 2023.06.06 |




