| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- shader programming
- Mesh Processing
- Graphics
- 컴퓨터 아키텍쳐
- shader
- OpenGL
- 윈도우
- 렌더링
- 그래픽스기초
- modeling
- 윈도우 구조
- win32
- c4d
- 컴퓨터 구조
- Geometry Modeling
- 오픈지엘
- MFC 윈도우 프로그래밍
- 셰이더프로그래밍
- 운영체제
- MFC
- 그래픽스
- Win32 API
- bezier curve
- 윈도우 프로그래밍
- 셰이더
- window programming
- 베지에 곡선
- 핵심 API로 배우는 윈도우프로그래밍
- denoising
- 윈도우프로그래밍
- Today
- Total
오다기리 박의 알고리즘 노트
허밋 스플라인 (Hermite Spline) 본문
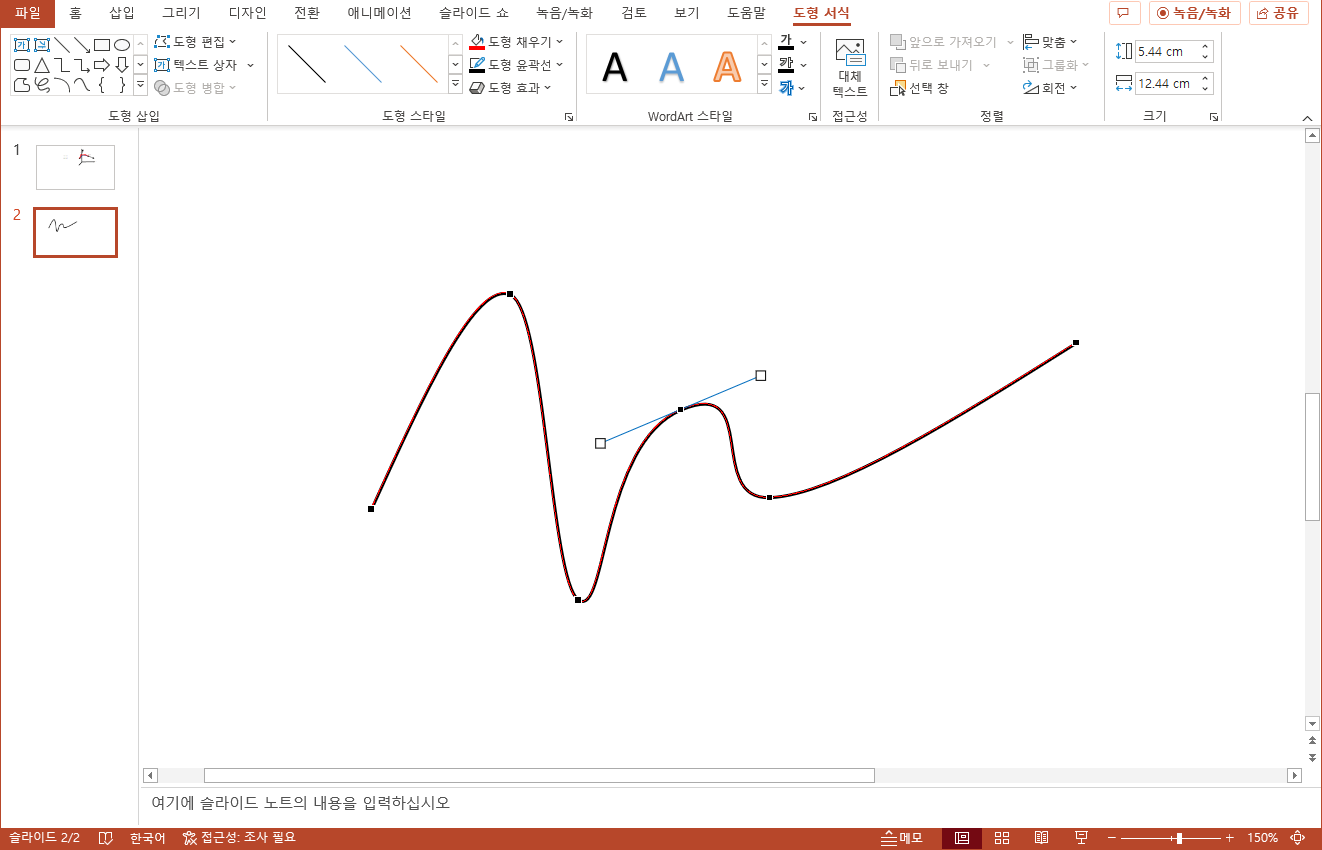
Hermite Spline 또는 Hermite Interpolation Curve는 곡선을 여러개 이어붙여 만든 스플라인을 말한다. 여기서는 일반적으로 많이 사용되는 방식에 대해 알아볼건데, 각 구간이 3차 베지에 곡선으로 구성되는 허밋 스플라인에 대한 내용이다.
스플라인의 어떤 한 구간에서 베지에 곡선 C(t)를 정의하기 위해서는 양 끝의 두 점 p0, p1과 접벡터(tangent vector) v0, v1가 필요하다. 그래야 스플라인의 각 보간점(Interpolation Point)에서 곡선이 기울기를 유지하며 부드럽게 이어질 수 있다. 여기서 각 곡선의 파라미터 범위는 [0, 1] 이다.
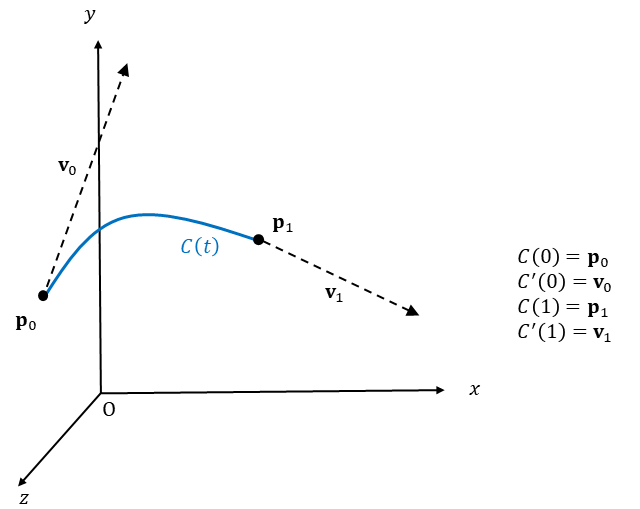
이렇게 주어진 양끝의 보간점과 접벡터로 식 C(t)를 어떻게 세울까? 3차 베지에 곡선 식을 세워야 하기 때문에 4개의 제어점(control point)을 b0, b1, b2, b3라고 한다면 얘네들을 4개의 번스타인 기저(Bernstein basis)와 선형 결합해야 한다.
베지에 곡선의 주요 성질 중 하나가 양 끝점에서의 접벡터는 인접한 두 제어점의 차이벡터의 3배와 같다는 것이다.(베지에 곡선 다항식을 미분하여 t = 0과 t = 1을 대입해보면 자연스럽게 유도된다.) 다시 말해서 v0 = 3(b1 - b0)이고 v1 = 3(b3 - b2)이다.
b0, b3은 두 보간점 p0, p1과 위치가 같다는 사실과 접벡터 공식을 이용하면 제어점의 위치를 모두 알아낼 수 있다.

결론적으로, 허밋 스플라인에서 한 구간의 양 끝점이 p0, p1이고 접벡터가 v0, v1으로 주어진 경우 베지에 곡선 C(t)는 다음과 같이 계산된다.

이렇게 보간점 한 쌍을 지나는 베지에 곡선을 만들 수 있으면 여러개의 보간점을 지나는 허밋 스플라인은 베지에 곡선을 이어붙여서 생성하면 된다. 각 보간점에서의 접벡터는 양 옆에 있는 보간점의 차이벡터로 계산할 수도 있고 사용자에 따라 임의로 조절할 수도 있다.
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 평면으로 폴리곤 자르기 (split polygon against plane) (0) | 2022.12.06 |
|---|---|
| 이진 공간 분할 트리 (BSP Tree) (0) | 2022.10.13 |
| 벡터를 평면에 사영(Projection)하기 (0) | 2022.08.17 |
| 벡터를 벡터에 사영(Projection)하기 (0) | 2022.08.17 |
| de Casteljau 알고리즘 (0) | 2022.08.12 |




