| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 윈도우프로그래밍
- 컴퓨터 아키텍쳐
- 그래픽스기초
- modeling
- 셰이더프로그래밍
- shader programming
- 윈도우
- 윈도우 구조
- 그래픽스
- 컴퓨터 구조
- c4d
- MFC
- 베지에 곡선
- 오픈지엘
- win32
- MFC 윈도우 프로그래밍
- 셰이더
- Mesh Processing
- Geometry Modeling
- 렌더링
- 윈도우 프로그래밍
- window programming
- 운영체제
- Win32 API
- denoising
- OpenGL
- shader
- Graphics
- 핵심 API로 배우는 윈도우프로그래밍
- bezier curve
- Today
- Total
오다기리 박의 알고리즘 노트
이진 공간 분할 트리 (BSP Tree) 본문
BSP 트리란?
이진 공간 분할법(Binary Space Partitioning)은 재귀적으로 3차원 공간을 평면으로 분할하는 기법이다. 분할 과정으로 BSP 트리라 불리는 트리 구조가 만들어진다. BSP 트리는 컴퓨터 그래픽스에서 렌더링 효율을 높이기 위해서 도입되었지만, CAD에서의 CSG(Constructive Solid Geometry), 충돌 감지(collision detection)에도 쓰기 좋다. 또한 폴리곤 메쉬의 내/외부를 구분하기에도 좋다. BSP 트리는 쿼드트리, 옥트리, k-d 트리와 비슷하지만 보다 더 일반적인 구조이다.
분할하는 공간이 n차원이면 분할 평면은 (n - 1)차원 초평면이다. 초평면은 평면의 일반화된 개념이라 생각하면 된다. 분할하고자하는 공간이 3차원이면 분할 초평면은 2차원 평면이고 공간이 2차원이라면 분할 초평면은 1차원 선이 된다. 또한 초평면에 의해 분할되는 공간은 (+) 공간과 (-) 공간으로 나뉜다. (+) 공간은 분할 평면의 위쪽, (-) 공간은 아래쪽을 말한다.

예를 들면 아래 그림 처럼 사각형 공간이 첫번째 초평면(이 경우에는 선) A에 의해 분할된다. 이 때 BSP 트리는 1개의 내부노드(원)과 2개의 리프노드(사각형)으로 구성된다. 두번째 초평면 B에 의해 노드 A의 - 공간이 분할된다. 마지막 초평면 C는 노드 A의 + 공간을 분할한다. 중요한 점은 리프 노드의 공간은 항상 convex하다는 것이다. 이 공간을 "셀"이라고 부르기도 한다. 초기 공간이 convex하다면 트리의 모든 공간도 convex하게 만들어진다.

아래 그림처럼 각각의 분할평면이 입력 폴리곤의 면에 해당되도록 설계하면 임의의 한 점이 폴리곤의 내/외부에 위치하는지 빠르게 판단할 수도 있다. 이런 경우를 autopartitioning 또는 polygon aligend 라고 부르기도 한다. 분할평면이 폴리곤 면이 아니라 xy, xz, yz 평면에 평행한 경우는 axis aligend 라고 부른다. axis aligend 평면만 사용하는 BSP 트리가 바로 k-d 트리이고 딱히 제약이 없는 경우가 일반적인 BSP 트리이다.

하나의 BSP 트리를 구성하는 시간이 꽤 걸리기 때문에 정적인 형태로 많이 사용한다. 움직이는 메쉬에 대해 실시간으로 BSP를 업데이트하려면 다른 특별한 방법을 써야한다.
Solid-leaf BSP Tree
BSP 트리는 분할평면의 방향, 기하 객체가 어떤 노드에 저장되는지, 트리가 공간 분할에 사용되는지 볼륨 표현에 사용되는지 등과 같은 다양한 기준에 의해 분류될 수 있다. node-storing, leaf-storing, solid-leaf 3가지 유형으로 나눌 수 있지만 이 글에서는 solid-leaf 유형에 대해서만 설명한다.
solid-leaf BSP 트리는 입력 기하 객체의 솔리드 볼륨을 표현하기 위해 구축되는 유형이다. 분할 평면들이 기하 객체의 내/외부를 정확히 구분한다. 아래 그림은 solid-leaf BSP 트리가 오목한 다각형 객체의 내부를 표현하는 것을 보여준다. 분할 평면이 곧 면이 포함된 평면이다. 균형 잡힌 트리를 구성하기 위해서는 오목한 정점을 포함한 평면을 분할 평면으로 시작하는게 좋다.
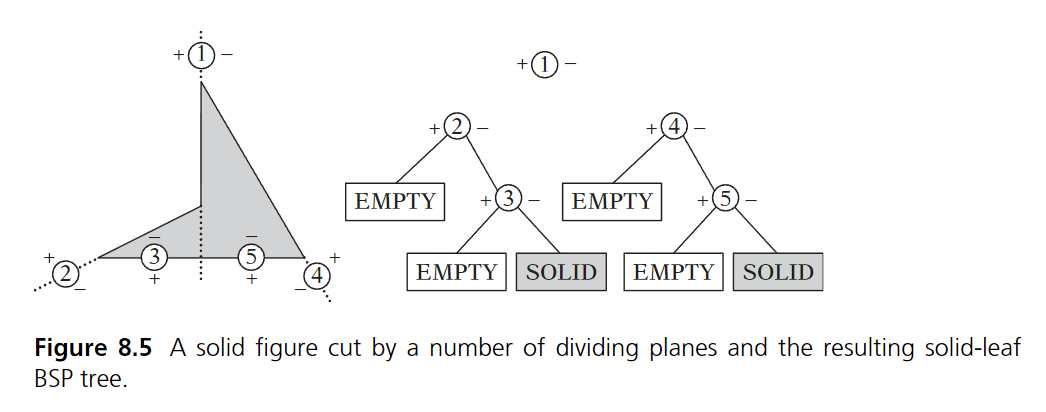
이 트리의 중요한 특징은 기하 객체(메쉬)가 트리 노드에 저장되지 않는다는 것이다. 리프 노드는 분할 평면의 양쪽 영역이 메쉬의 내부인지 외부인지 정도만 저장하고 있다. 다시 말해 트리가 입력 객체를 convex한 다면체의 집합으로 분할하며 각 다면체는 다수의 halspace의 교차영역이 된다.
이 방식을 사용하면 메쉬의 내/외부를 정확히 구분할 수 있기 때문에 메쉬 불리언 연산 등에 사용하기 좋다. 여기서는 solid-leaf BSP 트리를 중점적으로 살펴본다.
BSP 트리 만들기
BSP 트리를 만드는 과정은 다음 3가지 스텝을 밟는다.
- 분할 평면 선택
- 입력 기하 객체(메쉬)를 분할 평면 기준으로 둘로 나누기. 이 때 평면에 걸쳐있는 폴리곤들은 평면에 의해 잘린다.
- 이전 스텝에서 얻은 두 집합으로 트리 생성 알고리즘을 재귀호출하고 그렇게 생성된 두 하위 트리를 새 트리 노드와 연결한다.
여기서 중요한 연산이 몇가지 있다. 분할 평면을 선택하는 것, 메쉬를 분할 평면 기준으로 양쪽으로 나눌 때 각각의 폴리곤들이 평면 기준으로 어느 쪽에 위치하는지 판별하는 것, 걸쳐있는 폴리곤을 평면을 기준으로 자르는 것 등이다. 그리고 남아 있는 입력 폴리곤이 없을 때 트리 생성을 중단하는 것도 중요하다.
1. 분할 평면 만들기
트리를 생성할 때, 분할 평면을 선택하는게 중요한 이유는 결과 트리의 형태나 사이즈에 영향을 주어서 결국 트리에 대한 쿼리(query)를 수행할 때 큰 영향을 미치기 때문이다.
분할 평면을 선택하는 가장 단순한 방법은 자동 분할법인데, 메쉬를 구성하는 각 폴리곤을 분할 평면으로 잡는 것이다. 하지만 자동 분할법은 아래 그림의 왼쪽처럼 다른 폴리곤이 과도하게 잘리는(split) 단점이 있다. 하지만 임의의 평면을 분할 평면으로 사용하면 오른쪽처럼 불필요한 split 없이 폴리곤 그룹을 적절히 나눌 수 있다.
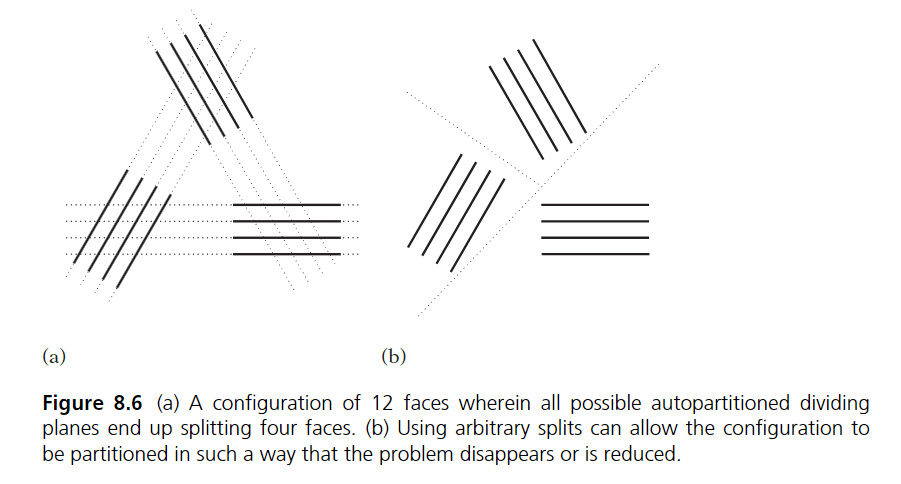
자동 분할법이 적절하지 않은 경우가 하나 더 있다. 구 메쉬로부터 BSP를 구성한다고 생각해보자. 구는 모든 면이 convex하기 때문에 어떤 면을 잡고 분할 평면을 만들더라도 다른 모든 면이 분할 평면 기준으로 한쪽에만 위치하게 된다. 이렇게되면 트리의 깊이(depth)는 폴리곤 수만큼 늘어나고 결국 BSP 트리는 매우 불균형적으로 될 것이다(아래 그림(a)). 더군다나 한 점이 메쉬 내/외부에 위치하는지 판단하기 위해 트리에 대한 쿼리를 수행하면 시간 복잡도는 O(n)이 될 것이다.
반면 그림(b) 처럼 분할 평면이 구를 가로지르도록 하는 임의 분할법을 사용하면 트리의 시간 복잡도는 O(log n)으로 나아진다. 하지만 BSP가 메쉬의 외면을 정확히 표현하려면 분할 평면이 이렇게 임의의 평면으로 표현되면 안된다. 다시 말해서 메쉬의 각각의 폴리곤으로 분할 평면을 만들어야 한다.
메쉬의 어떤 폴리곤이 분할 평면으로 만들기 좋을까?
(1) 다른 폴리곤들을 최소로 자를(split) 수록 (= 평면에 걸치는 폴리곤이 적을 수록)
(2) 메쉬를 비슷한 사이즈로 자를(split) 수록 (= 균형잡힌 트리가 만들어질 수록)
좋은 분할 평면이 된다. 하지만 조건 (1)만 따지면 트리가 불균형으로 만들어지고, 조건 (2)만 따지면 폴리곤이 너무 많이 잘리기 때문에 두 조건을 같이 고려해서 분할 평면을 생성해야 한다. 일반적으로는 (1)번 조건에 가중치를 더 주는 경우가 많고 트리의 깊이에 따라 다르게 설정해도 된다.
예를 들어 아래 그림에서 분할 평면 A는 조건 (1)만을 따진 경우, B는 (2)만 따진 경우, C는 (1), (2) 모두 따진 경우라고 볼 수 있다.
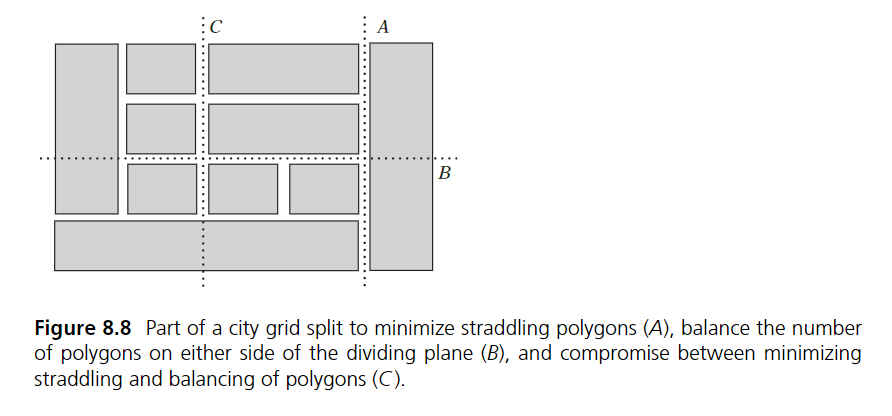
2. 평면에 대하여 폴리곤 위치 판단하기
분할 평면을 선택하고 만들었다면, 그걸 기준삼아 폴리곤 집합에서 각각의 폴리곤과 분할 평면과의 위치 판단을 한다. 분할 평면의 앞쪽(+)에 위치한 폴리곤 집합과 뒤쪽(-)에 위치한 폴리곤 집합을 각각 양쪽 자식노드로 전파시킨다. 폴리곤과 평면의 위치 관계를 참조하자.
3. 평면으로 폴리곤 자르기
BSP 트리가 만들어지는 과정에서 어떤 한 폴리곤이 분할 평면에 걸쳐있으면 그 폴리곤은 두 개로 잘리고(split), 각각 트리의 양쪽으로 내려간다. 아래 그림에서 삼각형 T가 잘리는 과정을 생각해보자. 1번 평면에 의해 먼저 잘리면 오른쪽 작은 폴리곤이 생기고, 작은 폴리곤은 2번 평면 기준으로 B공간으로 분류된다. (만약 폴리곤을 자르는 것을 무시해 버린다면, T의 복사본이 이곳 저곳에 존재할 것이다.) 자세한 알고리즘은 평면으로 폴리곤 자르기를 참조하자.

BSP 트리 사용하기
공간상의 임의의 점이 메쉬의 내부에 있는지 외부에 있는지 검사할 때 BSP 트리를 많이 사용한다. 각각의 노드에 대해서 점이 평면의 어느쪽에 위치하는지 쉽게 알 수 있기 때문이다. 점이 어떤 분할 평면의 앞에 위치하면 앞쪽 자식 노드를 방문하면 된다. 이러한 검사를 리프노드를 만날 때까지 반복하기만 하면 된다.
[심화] BSP 트리 집합 연산
나아가 두 BSP 트리를 서로 merge하거나 reduction할 수도 있다. BSP 기반의 메쉬 불리언 연산(UNION, INTERSECTION, DEFFERENCE)을 하기 위해서는 이러한 집합 연산이 필요하다. 여기서 BSP 트리 사이의 집합 연산을 추가로 소개한다.
폴리곤 메쉬 P1, P2의 BSP 트리를 각각 T1, T2라고 할 때 두 트리를 merge 하는 것은 T1에 T2를 삽입하는 것이라고 보면 된다. T1의 루트 노드에서 시작해서 T2가 T1의 리프 노드에 도달할 때까지 재귀적으로 삽입된다. 삽입될 때마다 트리 T2는 T1의 각 노드에 의해 매번 분할된다. 재귀 프로세스는 다음 순서로 진행된다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
1. 삽입되는 노드가 리프노드라면 그냥 합친다.(?)
2. t1과 T2의 공통 영역(?)에서 ht1와 hT2의 상대적인 위치를 계산한다.
공통 영역에서 두 평면의 위치 관계는 총 7케이스가 나온다.
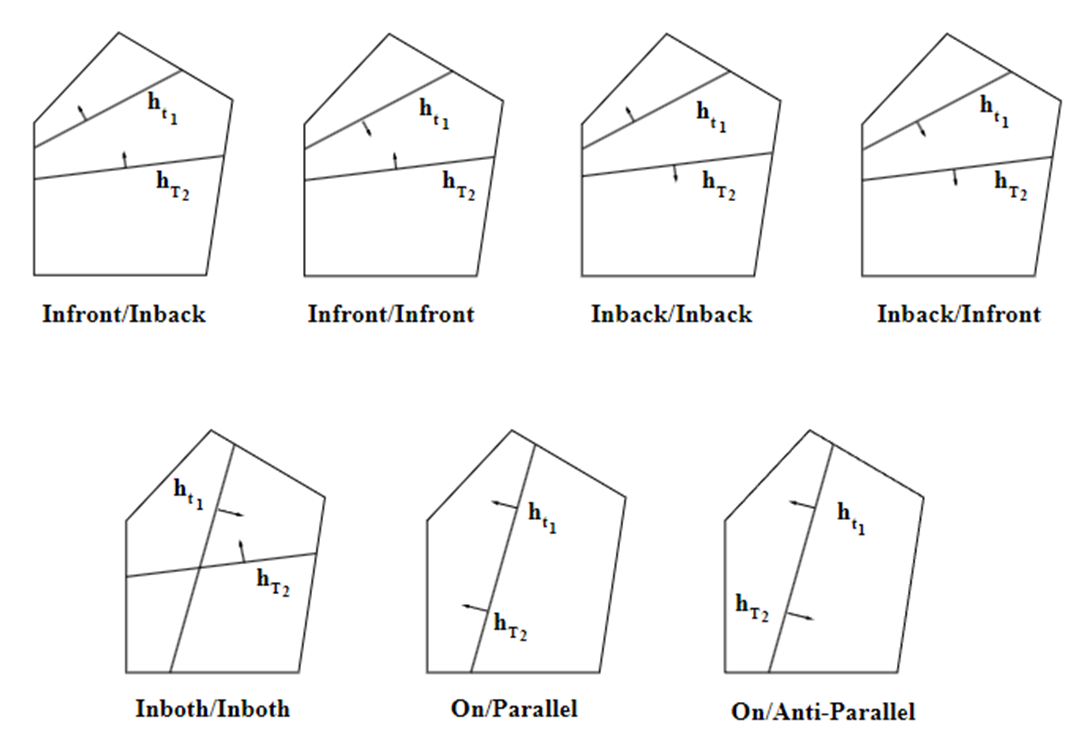
3. T2의 서브트리를 ht1에 대하여 T2+와 T2-로 나눈다.
이 때 ht1이 놓인 서브트리만 분할된다.
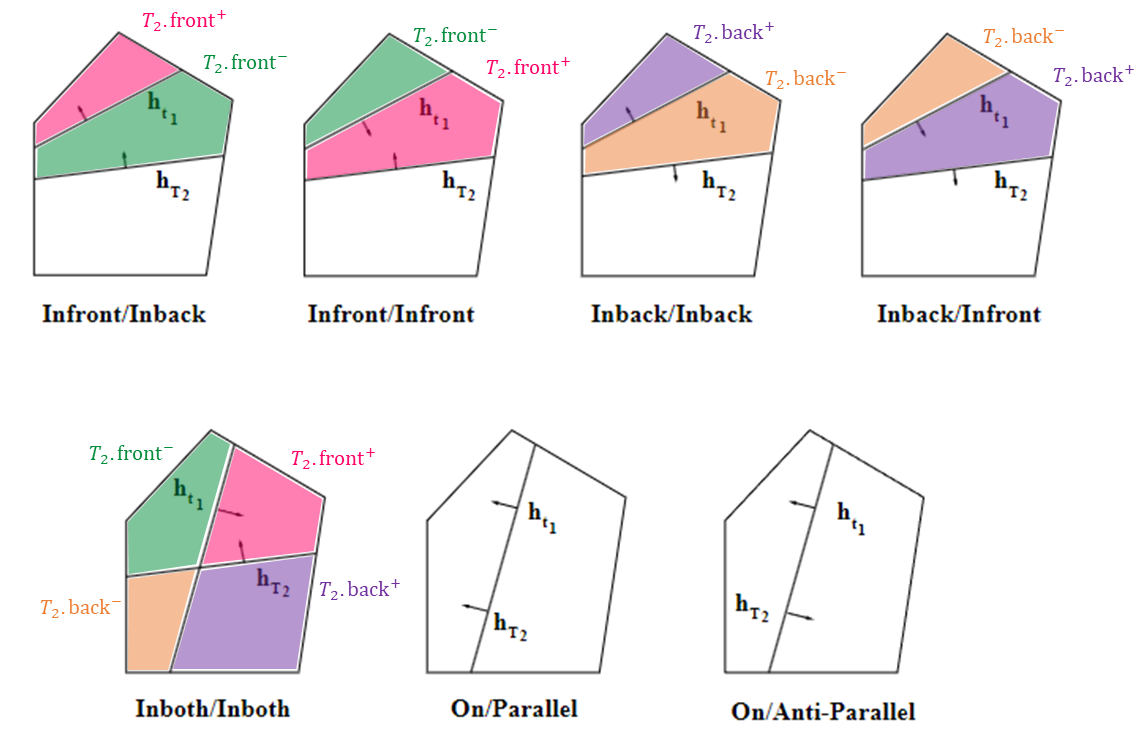
4. T2+는 t1.front에, T2-는 t1.back에 재귀적으로 삽입된다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
결론적으로 다음과 같이 pseudo-code로 나타낼 수 있다. 2 ~ 3 과정이 partitionTree() 함수 안에서 수행된다.

그리고 다음 테이블이 treeOpCell() 함수의 역할을 보여준다.

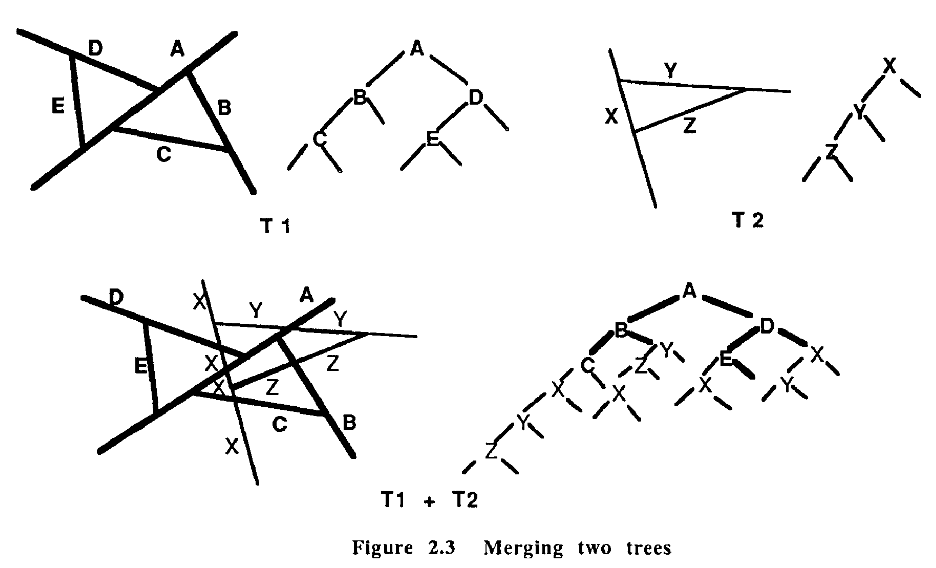
아래 그림은 두 트리 T1 ,T2가 merge되는 예시이다.
[심화] BSP 트리로부터 메쉬 만들기
메쉬로부터 BSP 트리가 만들어진 아래 예시를 살펴보자.
(a)에서 하얀색 영역은 OUT(empty) 상태인 리프 노드의 셀을 나타내고 파란색 영역은 IN(soild) 상태인 리프 노드의 셀을 나타낸다. 각 영역은 메쉬의 바운딩 박스 내에서 표현된다.
(b)에서는 IN 상태의 셀의 각 면을 보여준다. 이론적으로 IN 셀을 모아서 합치면 메쉬를 만들 수 있다. 하지만 빨간색으로 표시된 부분처럼 중복된 면이 생길 수가 있다.
(c)에서 중복 면을 골라서 없애야만 (d)처럼 완전한 메쉬로 만들 수 있다.
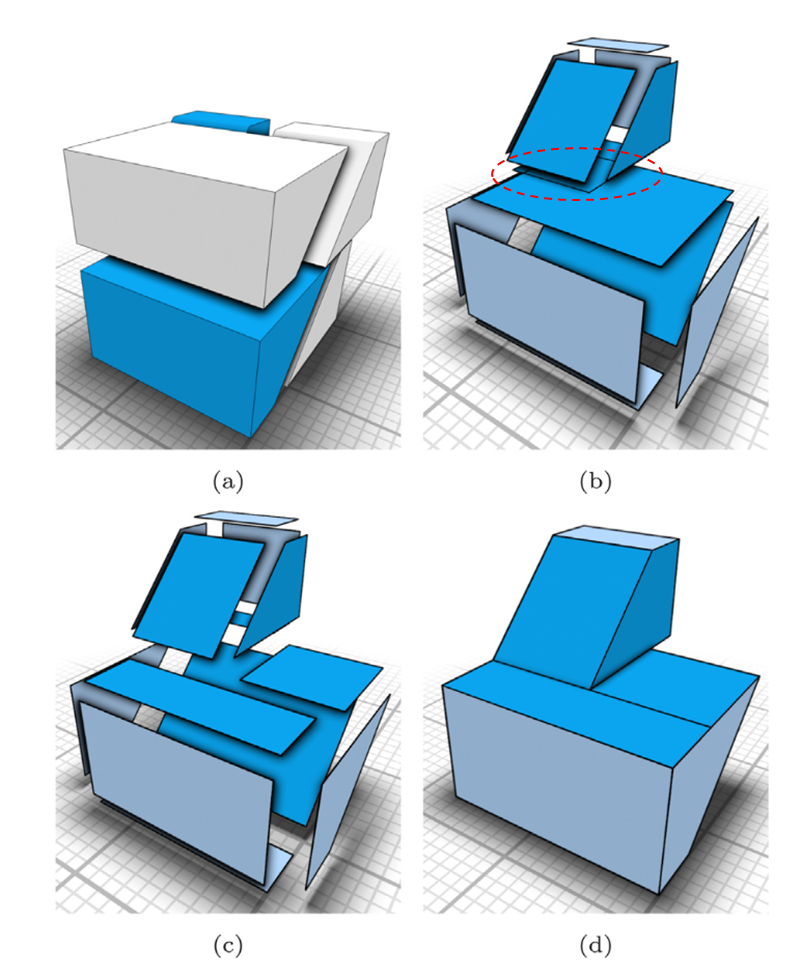
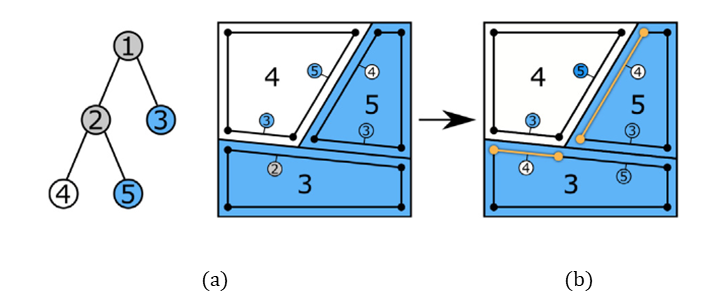
그렇다면 중복되는 면 없이 IN 상태의 리프 노드의 셀을 구하려면 어떻게 해야 할까? 리프 노드까지 내려가며 방문되는 노드의 분할 평면으로 메쉬의 바운딩 박스를 반복 분할하면 된다. BSP 트리를 참고하며 바운딩 박스를 분할해가는 아래 예시를 보자.
(a)를 보면 우선 전체 바운딩 영역 1은 평면 1에 의해 영역 2와 3으로 나뉜다. 영역 3은 리프 노드가 되고 영역 2는 평면 2에 의해 영역 4와 영역 5로 한번 더 나뉜다. 이 때 중요한 것은 매 분할마다 평면 양쪽에 생기는 폴리곤에다가 반대편 영역을 나타내는 노드 번호(작은 번호로 레이블링 되어 있음)를 표기하는 것이다. 그리고 표기되어 있는 노드가 리프 노드가 아닌 폴리곤은 표기되어 있는 노드의 평면으로 한번더 분할해야 한다. 노드 2가 레이블링 되어있는 폴리곤이 평면 2로 한번 더 분할되어 각각 노드 4, 노드 5로 다시 레이블링 되어있는 것을 (b)에서 볼 수 있다. 결과적으로 IN-IN 으로 표기되어 있는 면이 없애야할 부분이다.
[참고]
[1] Ericson, Christer. Real-time collision detection. Crc Press, 2004.
[2] Chrysanthou, Yiorgos L. "A Tutorial on Binary Space Partitioning Trees part of EG tutorial on visibility."
[3] Naylor, Bruce, John Amanatides, and William Thibault. "Merging BSP trees yields polyhedral set operations." ACM Siggraph Computer Graphics 24.4 (1990): 115-124.
[4] Nehring-Wirxel, Julius, Philip Trettner, and Leif Kobbelt. "Fast exact booleans for iterated CSG using octree-embedded BSPs." Computer-Aided Design 135 (2021): 103015.
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 평면 기반 폴리곤 표현법 (plane-based polygon) (2) | 2022.12.06 |
|---|---|
| 평면으로 폴리곤 자르기 (split polygon against plane) (0) | 2022.12.06 |
| 허밋 스플라인 (Hermite Spline) (0) | 2022.08.22 |
| 벡터를 평면에 사영(Projection)하기 (0) | 2022.08.17 |
| 벡터를 벡터에 사영(Projection)하기 (0) | 2022.08.17 |




