| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- c4d
- 컴퓨터 구조
- window programming
- bezier curve
- 셰이더
- 윈도우 구조
- 윈도우프로그래밍
- shader programming
- OpenGL
- denoising
- modeling
- 윈도우
- 핵심 API로 배우는 윈도우프로그래밍
- 윈도우 프로그래밍
- Mesh Processing
- 그래픽스
- Geometry Modeling
- 컴퓨터 아키텍쳐
- 베지에 곡선
- win32
- 셰이더프로그래밍
- 렌더링
- MFC
- 오픈지엘
- 운영체제
- shader
- MFC 윈도우 프로그래밍
- 그래픽스기초
- Win32 API
- Graphics
- Today
- Total
오다기리 박의 알고리즘 노트
평면으로 폴리곤 자르기 (split polygon against plane) 본문
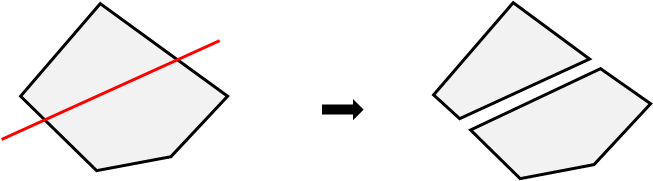
평면으로 폴리곤을 자르는 방법에 대해 알아보자. 메쉬를 측지선으로 자르거나 평면으로 잘라서 양쪽으로 분할하거나, 메쉬에 대한 BSP 트리를 만들 때 폴리곤을 평면으로 잘라야하는 경우가 많이 생긴다. 여기서는 명시적(explicit) 방법과 암시적(implicit) 방법으로 구분해서 설명한다.
1. Explicit Split
폴리곤이 평면으로 잘려서 두 폴리곤으로 나뉜다고 할 때, 명시적 방법은 두 폴리곤의 꼭지점을 직접 계산하는 방법이다. CAD 프로그래밍을 할 때에는 수치오류를 고려하여 평면에 두께를 주는편이 좋다. 다시 말해서 점이 평면의 두께 안에만 들어온다면 점은 평면에 포함된다고 간주한다.
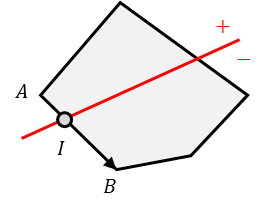
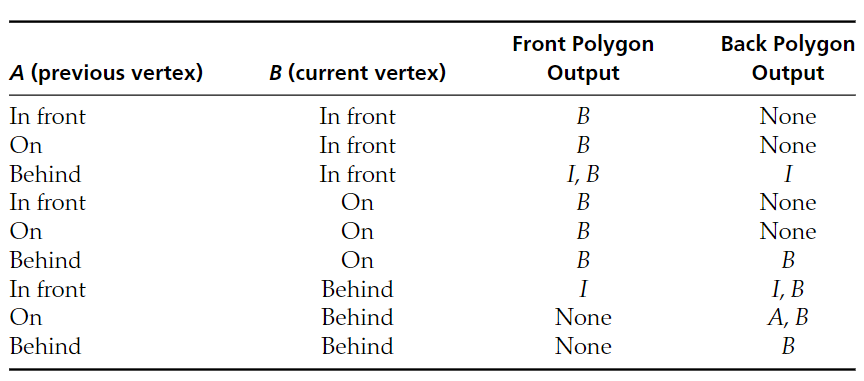
다음 그림처럼 폴리곤의 한 에지에 대하여 시작점을 A, 끝점을 B 라고 하고 두 점의 위치를 테이블에서 참조해본다. (테이블은 Sutherland–Hodgman 알고리즘을 조금 보완한 버전이다.) 그림에서는 A 가 평면 앞, B 가 평면 뒤에 있으니 (+) 폴리곤의 정점에는 교차점 I 가 추가되고, (-) 폴리곤의 정점에는 I 와 B 가 추가된다. 폴리곤의 모든 에지를 순환하며 테이블을 참조하면 평면 기준 (+) 폴리곤의 정점 리스트와 (-) 폴리곤의 정점 리스트를 구성할 수 있게 된다.
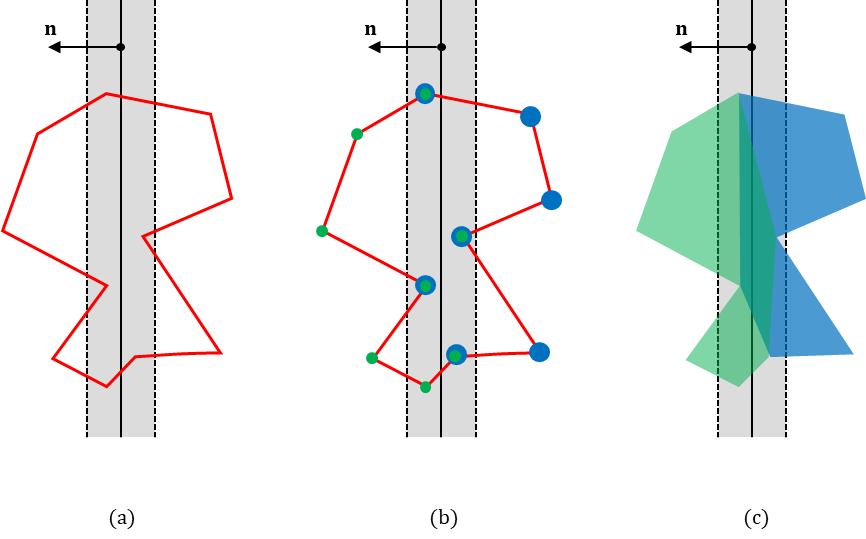
아래 그림 (a)에서 빨간색 폴리곤이 두께가 있는 평면에 걸친 상태에서 폴리곤을 두 개로 잘라서 분할 해보자. 폴리곤 각각의 에지를 반시계 방향으로 순회하면서 테이블 규칙을 적용하면 (b)와 같이 왼쪽 부분 폴리곤 정점(초록), 오른쪽 부분 폴리곤 정점(파랑)이 생성된다. 이 정점으로 두 개의 새로운 폴리곤을 생성하면 (c)와 같이 된다.
2. Implicit Split
폴리곤을 명시적으로 자를 때에는 평면과 폴리곤의 교차점을 계산해야 하기 때문에 반복 수행하면 수치오차가 누적될 수 밖에 없다.
그리고 두 폴리곤이 붙어있는 상황에서 각각의 폴리곤을 평면으로 자르려고 하면 공통된 에지에서 수치 오차가 발생할 수도 있다. 예를 들면 아래 그림처럼 폴리곤 ABC와 CBD를 각각 분할 했는데 에지 BC에서 어긋나는 경우이다.
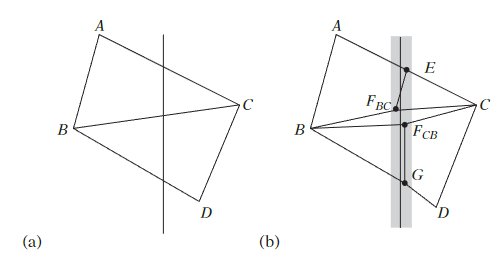
대신에 평면 기반 폴리곤(plane-based polygon) 표현법을 사용하면 수치오차를 어느정도 해결할 수 있다. 평면 기반 폴리곤 표현법은 convex 폴리곤을 평면 s 위에서 경계 평면 { bi } i∈Zn 으로 둘러쌓인 영역으로 표현하는 것이다. (경계 평면은 반시계 방향 순서이다.)
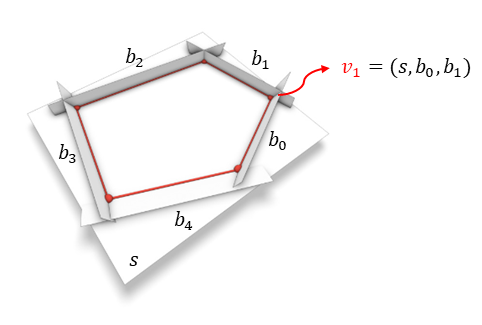
아래 그림은 폴리곤이 포함된 평면 s와 각 에지를 포함하면서 s에 직교하는 평면 5개를 나타낸다. 이렇게 되면 폴리곤의 각 점은 vi = (s, bi-1, bi) 로 표현할 수 있다. 즉 모든 점을 세 평면의 조합으로 표현할 수 있다. 점의 좌표를 계산하고 싶을 때에는 세 평면의 교차점을 계산하면 된다.
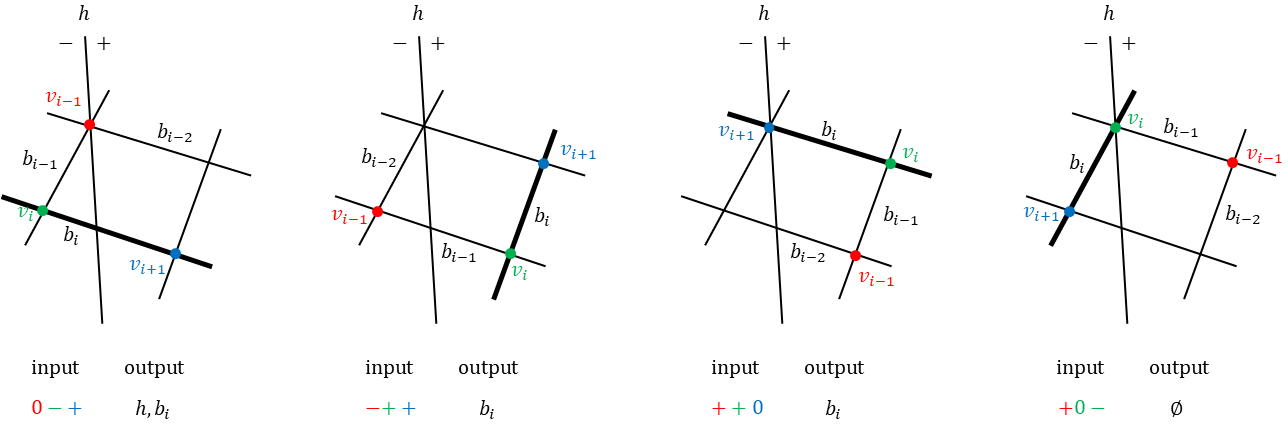
먼저 폴리곤 P (s, { bi } i∈Zn) 와 이를 자르는 어떤 분할 평면 h가 주어졌다고 하자. P를 h로 잘랐을 때 h의 (+) 방향에 위치하는 폴리곤을 먼저 구해보자. 먼저 폴리곤 각각의 경계 평면 bi 을 기준으로 삼고 점 vi-1, vi, vi+1이 h에 대해 아래에 있는지(-), 포함되어 있는지(0), 위에 있는지(+) 검사해본다.
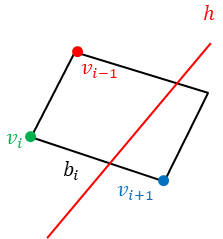
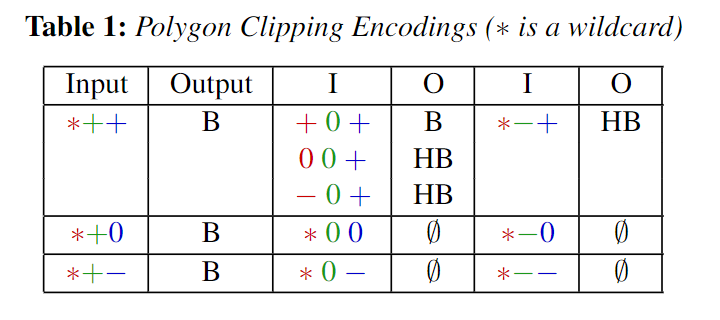
예를 들어 아래 그림의 첫번째 경우에는 점 vi-1, vi, vi+1이 h에 대해 각각 0,-,+의 상태를 갖는다. 이 상태를 테이블에서 참조하면 두 평면 h, bi 모두 (+) 폴리곤을 구성하는 경계 평면이 된다.

평면 기반 폴리곤을 분할 평면으로 자르는 예를 하나 들어보자. 아래처럼 네 개의 경계 평면으로 표현된 폴리곤 P와 이것을 분할 평면 h가 자르는 상황이다.
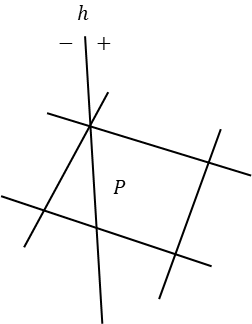
각각의 경계 평면을 bi로 잡고 h에 대한 주변 세 점의 부호를 테이블에서 참조하여 출력 평면을 선택한다.
이렇게 수집한 출력 평면을 모두 모아보면,
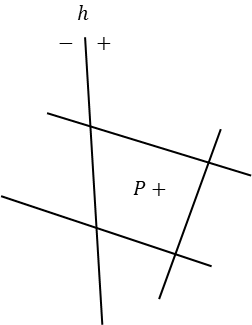
분할 평면 h의 (+) 폴리곤의 경계 평면을 반시계 방향으로 구할 수 있다. (-)부분은 테이블을 변형해서 사용해야 한다.
[참고]
[1] Bernstein, Gilbert, and Don Fussell. "Fast, exact, linear booleans." Computer Graphics Forum. Vol. 28. No. 5. Oxford, UK: Blackwell Publishing Ltd, 2009.
[2] Ericson, Christer. Real-time collision detection. Crc Press, 2004.
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 폴리곤과 평면의 위치 관계 (0) | 2022.12.06 |
|---|---|
| 평면 기반 폴리곤 표현법 (plane-based polygon) (2) | 2022.12.06 |
| 이진 공간 분할 트리 (BSP Tree) (0) | 2022.10.13 |
| 허밋 스플라인 (Hermite Spline) (0) | 2022.08.22 |
| 벡터를 평면에 사영(Projection)하기 (0) | 2022.08.17 |




