| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 윈도우프로그래밍
- denoising
- 컴퓨터 구조
- Win32 API
- 베지에 곡선
- bezier curve
- MFC 윈도우 프로그래밍
- 오픈지엘
- 윈도우 프로그래밍
- 컴퓨터 아키텍쳐
- 윈도우
- Mesh Processing
- win32
- 셰이더프로그래밍
- c4d
- modeling
- 렌더링
- Geometry Modeling
- window programming
- 그래픽스
- 셰이더
- MFC
- Graphics
- OpenGL
- shader
- 핵심 API로 배우는 윈도우프로그래밍
- 운영체제
- 그래픽스기초
- 윈도우 구조
- shader programming
Archives
- Today
- Total
오다기리 박의 알고리즘 노트
벡터를 벡터에 사영(Projection)하기 본문
3차원 공간에서 a벡터를 b벡터에 사영(projection)하여 c벡터를 구해보자.
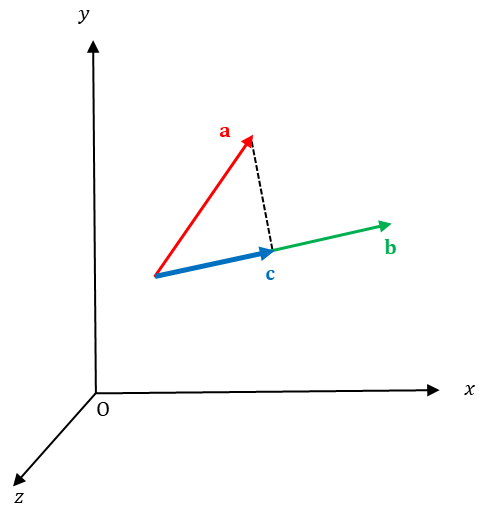
c를 구하려면 길이와 방향이 필요하다.
c의 길이는 a와 b를 내적하여 b의 길이로 나눈 값과 같다. 즉 a와 b의 사잇각이 θ일 때 a와 b의 내적값은 ||a||||b||cosθ이고 이 값을 b의 길이로 나눈다.

c의 방향은 b를 정규화하면 된다.
결론적으로 위에서 구한 c의 길이와 방향을 곱하면 사영벡터 c가 계산된다.

'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 허밋 스플라인 (Hermite Spline) (0) | 2022.08.22 |
|---|---|
| 벡터를 평면에 사영(Projection)하기 (0) | 2022.08.17 |
| de Casteljau 알고리즘 (0) | 2022.08.12 |
| 베지에 곡선 (Bézier Curve) (0) | 2022.07.15 |
| 메쉬 위의 최단 측지 경로 (Shortest Geodesic Path on Meshes) (0) | 2022.06.14 |




