| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- window programming
- 윈도우 구조
- win32
- bezier curve
- 윈도우 프로그래밍
- 오픈지엘
- shader programming
- 셰이더
- 그래픽스
- 핵심 API로 배우는 윈도우프로그래밍
- c4d
- Geometry Modeling
- 컴퓨터 구조
- 윈도우프로그래밍
- MFC 윈도우 프로그래밍
- 셰이더프로그래밍
- Win32 API
- OpenGL
- denoising
- 베지에 곡선
- 윈도우
- modeling
- MFC
- Graphics
- Mesh Processing
- 그래픽스기초
- 컴퓨터 아키텍쳐
- 운영체제
- shader
- 렌더링
- Today
- Total
오다기리 박의 알고리즘 노트
매개변수 곡면 (Parametric Surface) 본문
3차원상의 곡면을 매개방정식으로 나타내보자. 곡면은 3개의 성분 각 성분은 2개의 매개변수 u, v에 대한 식으로 이루어져 있다. 곡면의 매개방정식은 함수

로 나타낸다. D는 2차원에 들어있는 정의역이다. 그러니까 2차원의 두 매개변수가 함수 φ를 통해서 3차원 공간의 곡면으로 변한다는 뜻이다. 이렇게 만들어진 곡면을 다음과 같이 표기한다.

만약 φ가 미분 가능하거나 C1 함수이면 S를 '미분가능한 곡면' 또는 'C1 곡면'이라고 한다.
접벡터
매개곡면 S가 (u0, v0) 에서 미분 가능할 때 이 점에서 곡면의 접벡터를 계산해보자. 곡면 위의 한 점에서 접평면을 정의하기 위해서는 접벡터를 알아야 하기 때문에 접벡터 먼저 짚고 넘어가도록 하자.
접벡터를 계산하기 위해서는 접벡터가 어느 방향을 향하는지 먼저 알아야 한다. 이를 위해 우선 u = u0로 고정하고 v는 임의의 값을 가진다고 하자. 그러면 곡면 위에 v 방향으로의 곡선이 그려진다. φ(u0, v0)에서 이 곡선의 접벡터를 Tv라고 하자.
마찬가지로 v = v0로 고정하고 u는 임의의 값을 가질 때 곡면 위에 u방향으로의 곡선이 그려진다. φ(u0, v0)에서 이 곡선의 접벡터를 Tu라고 하자.

Tv와 Tu는 각각 다음과 같이 계산된다.
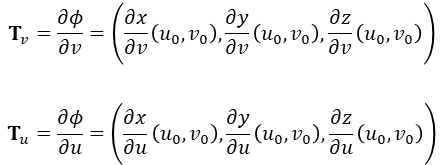
즉, Tv는 곡면 S를 v방향으로 편미분한 식에 u0, v0를 대입하여 구하고, Tu는 곡면 S를 u방향으로 편미분한 식에 u0, v0를 대입하여 구한다.
접평면
벡터 Tu와 Tv가 주어진 점에서 곡면의 두 곡선에 각각 접하기 때문에 Tu X Tv는 그 점에서 곡면에 수직이어야 한다. 곡면 위의 점 φ(u0, v0) = (x0, y0, z0)에서 접평면의 방정식은 다음과 같다.
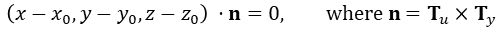
넓이
매개곡면 S의 넓이 A(S)는 다음과 같이 정의한다.
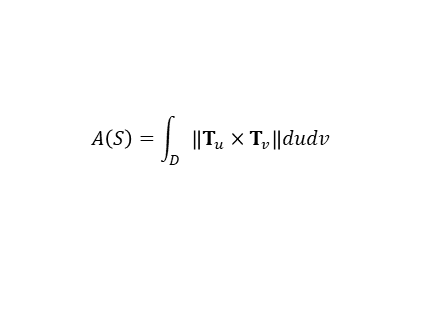
S가 곡면 Si들의 합집합이면 그 넓이는 Si의 넓이의 합이다.
넓이 (그래프 표현)
곡면의 식이 그래프의 형태로 주어졌다고 해보자. z = g(x, y), (x, y) ∈ D의 형태로 주어진 곡면 S의 좌표는 x = u, y = v, z = g(u, v) 와 같이 매개방정식 형태로 다시 표현할 수 있다. 이 때 (u, v) ∈ D 이다. S의 임의의 점에서 u 방향, v 방향 접벡터는 다음과 같다.
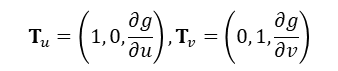
그리고 다음과 같이 법선 벡터 n과 그 크기는 두 접벡터로부터 계산됨을 알 수 있다.
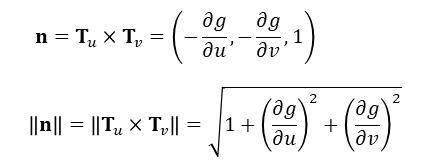
g가 C1함수이면 매개방정식은 매끄러우며 곡면의 넓이는 다음과 같다.
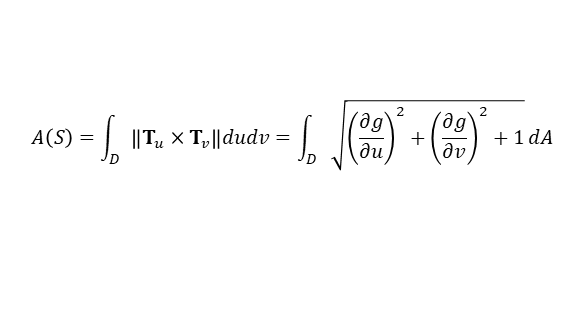
결론적으로 곡면의 넓이는 곡면의 법선 벡터의 크기를 도메인 영역에 대하여 적분한 값이라고 생각할 수 있다.
이렇게 곡면의 넓이를 구하기 위해서는 매개변수 표현식, 즉 매개곡면으로 나타내는 것이 좋다.
'미적분학' 카테고리의 다른 글
| 그린 정리(Green's Theorem) (0) | 2023.02.26 |
|---|---|
| 면적분 (Surface Integral) (0) | 2022.10.10 |
| 선적분(Line Integral) (2) | 2022.09.20 |
| 미분연산자: 그래디언트(Gradient), 발산(Divergence), 컬(Curl), 라플라시안(Laplacian) (0) | 2022.09.05 |
| 직교 좌표계(Orthogonal Coordinates), 원기둥좌표계(Cylindrical Coordinate System) , 구면과표계(Spherical Coordinates) (0) | 2022.08.20 |




