| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 윈도우 구조
- Graphics
- 그래픽스기초
- Win32 API
- modeling
- 베지에 곡선
- 컴퓨터 아키텍쳐
- 오픈지엘
- 윈도우프로그래밍
- 윈도우
- win32
- shader
- Mesh Processing
- 셰이더프로그래밍
- MFC
- denoising
- window programming
- shader programming
- 윈도우 프로그래밍
- OpenGL
- bezier curve
- 렌더링
- MFC 윈도우 프로그래밍
- Geometry Modeling
- 셰이더
- 컴퓨터 구조
- 운영체제
- c4d
- 그래픽스
- 핵심 API로 배우는 윈도우프로그래밍
Archives
- Today
- Total
오다기리 박의 알고리즘 노트
메쉬 위의 최단 측지 경로 (Shortest Geodesic Path on Meshes) 본문
메쉬 위에서 두 점을 잇는 최단 경로를 구하는 방법에 대해 알아보자.
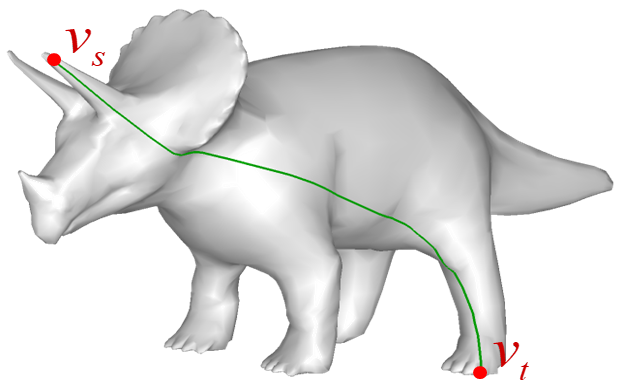
사실 측지 경로를 구하는 문제는 컴퓨터 그래픽스에서 많이 사용된다. 메쉬 측지선으로 메쉬 분할(Segmetation), 자르기(Cutting)가 가능하다. 또한 여러 알고리즘의 기반이 되는 곡면 위의 거리 측정에도 유용하다. 예를 들면 메쉬 위에서 방사형 기저 선형보간( Radial-Basis Interpolation)을 계산하려면 측지거리를 계산해야 되며 이런 기법이 스키닝(skinning), 메쉬 워터마킹(mesh watermarking), 곡면 벡터장(vector field)을 정의하는 등 여러 어플리케이션에서 사용된다.
여기서 소개할 알고리즘은 소스점 s를 고정하고 다른 모든 정점까지의 최단 거리장을 먼저 구한 다음 이에 기반하여 교차점을 추적하여 최단 경로를 구성하는 방식이다. 교차점을 추적하는 규칙은 다음과 같다.
- 만약 현재 교차점이 정점에 위치한다면 1-Ring 경계 에지 중에서 시작 교차점을 찾는다.
- 만약 현재 교차점이 에지에 위치한다면 주변 4개의 에지 중에서 시작 교차점을 찾는다.
- 만약 현재 교차점이 삼각형 내부에 위치한다면 주변 3개의 에지 중에서 시작 교차점을 찾는다.
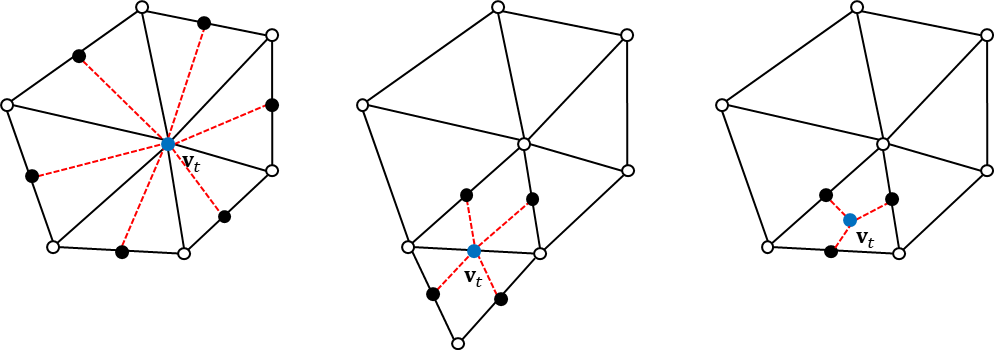
교차점을 추적하는 규칙을 이용해서 알고리즘을 살펴보자.
알고리즘
- 소스점 s와 타겟점 t를 정한다.
- s에서 t까지 거리 이내의 최단 거리장을 구성한다.
- 교차점 추적 규칙에 의해 t에서 s로 향하는 시작 교차점을 찾는다.
- 교차점 추적 규칙에 의해 현재 교차점에서 다음 교차점을 찾는다.
- 현재 교차점이 s의 주변 정점/주변 에지에 도달할 때까지 과정 4를 반복한다.
[참고] Surazhsky, Vitaly, et al. "Fast exact and approximate geodesics on meshes." ACM transactions on graphics (TOG)
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| de Casteljau 알고리즘 (0) | 2022.08.12 |
|---|---|
| 베지에 곡선 (Bézier Curve) (0) | 2022.07.15 |
| Non-Manifold Topology 메쉬 (0) | 2022.06.10 |
| 이산 가우스 곡률(Discrete Gauss Curvature) (0) | 2022.05.11 |
| 메쉬 위의 측지 극좌표 (Geodesic Polar Coordinates on Polygonal Meshes) (0) | 2022.05.04 |




