| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 컴퓨터 아키텍쳐
- bezier curve
- shader programming
- 핵심 API로 배우는 윈도우프로그래밍
- Geometry Modeling
- 베지에 곡선
- 오픈지엘
- win32
- shader
- 그래픽스기초
- 컴퓨터 구조
- Mesh Processing
- Graphics
- 운영체제
- modeling
- MFC 윈도우 프로그래밍
- denoising
- window programming
- 윈도우
- Win32 API
- MFC
- 셰이더
- 윈도우프로그래밍
- 그래픽스
- 렌더링
- 윈도우 구조
- 셰이더프로그래밍
- OpenGL
- c4d
- 윈도우 프로그래밍
Archives
- Today
- Total
오다기리 박의 알고리즘 노트
이산 가우스 곡률(Discrete Gauss Curvature) 본문
메쉬 위에서 가우스 곡률(Gauss curvature)에 대해 알아보자. 정점 p 주변에 m개의 인접 삼각형이 있을 때, 다음과 같이 2π에서 정점 주변각의 합을 뺀값이 가우스 곡률이다.
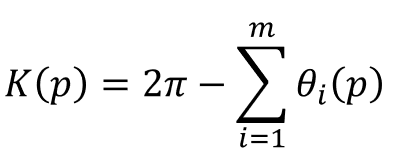
이 가우스 곡률에 따라 정점을 다음과 같이 3가지로 구분할 수 있다. 예를 들어 정육면체의 각 정점은 가우스 곡률이 π/2과 같다.
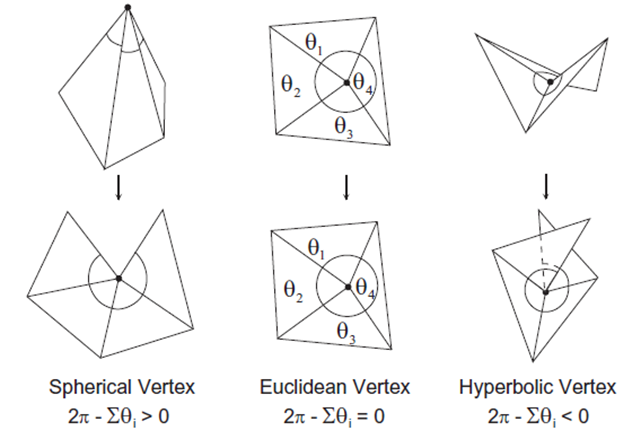
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 메쉬 위의 최단 측지 경로 (Shortest Geodesic Path on Meshes) (0) | 2022.06.14 |
|---|---|
| Non-Manifold Topology 메쉬 (0) | 2022.06.10 |
| 메쉬 위의 측지 극좌표 (Geodesic Polar Coordinates on Polygonal Meshes) (0) | 2022.05.04 |
| 직선과 다각형의 교차점 구하기 (0) | 2022.03.16 |
| BVH(Bounding Volume Hierarchy) (1) | 2022.03.15 |




