| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- window programming
- 그래픽스
- 렌더링
- c4d
- 운영체제
- 컴퓨터 아키텍쳐
- 핵심 API로 배우는 윈도우프로그래밍
- 윈도우 프로그래밍
- shader programming
- modeling
- 그래픽스기초
- Geometry Modeling
- bezier curve
- win32
- 윈도우 구조
- 베지에 곡선
- 셰이더
- Graphics
- Win32 API
- shader
- 오픈지엘
- 윈도우프로그래밍
- denoising
- 컴퓨터 구조
- OpenGL
- MFC 윈도우 프로그래밍
- MFC
- 셰이더프로그래밍
- Mesh Processing
- 윈도우
- Today
- Total
오다기리 박의 알고리즘 노트
BVH(Bounding Volume Hierarchy) 본문
기하객체가 용량이 큰 경우 컴퓨터 그래픽스 렌더링과정에서 시간이 오래 걸린다. 이를 가속화 하기 위해 기하개체를 3차원 공간 안에서 구조화하는 Spatial Data Structure를 주로 사용한다.
Spatial Data Structure는 일반적으로 계층구조 (hierarchy)에 기반하여 구현한다. 계층구조는 부모/자식 노드로 구성되며 각 노드는 자신의 공간을 정의한다. 이런 구조를 이용해서 기하개체를 구성하는 각각의 요소에 빠르게 접근할 수 있다. Spatial Data Structure를 한번 생성하는 데 걸리는 시간은 기하개체의 용량, 구조의 퀄리티 등에 따라 좌우되므로 오래 걸릴 수도 있다.
Spatial Data Structure에는 BVH, BSP Tree, Octree 등이 있는데, BSP Tree와 Octree는 공간 분할(space subdivision)에 기반하여 만든다. 그러니까 공간 전체를 분할하여 데이터구조로 만드는 형태이기 때문에 모든 리프노드를 더하면 겹치는 부분 없이 공간 전체가 된다. BSP Tree는 공간 분할하는 크기가 불규칙하지만, Octree는 균등하게 분할한다. 반면 BVH는 기하개체를 감싸는 박스를 만들면서 공간이 아닌 기하개체를 분할하기 때문에 조금 다르다.
여기서는 BVH에 대해서 다뤄보기로 한다.
BVH는 직관적으로는 2차원, 3차원 공간에서 구성할 수 있지만 더 높은 차원에서도 사용할 수 있다. 주로 culling algorithm, intersection test, ray tracing, collision detection에 많이 사용된다. BVH에서 말하는 BV는 Bounding Volume을 얘기하는데, BV는 구가 될 수도 있고, AABB나 OBB 가 될 수도 있고, k-DOP가 될 수도 있다.
BVH를 구성하는 노드를 다음 세가지로 나눠볼 수 있다.
- root node : 최상단 노드
- internal node : 자식 노드를 가진 노드
- leaf node : 최하단 노드
계층구조에 root 하나만 딸랑 있는게 아니라면 root노드 또한 internal node가 될 것이다. leaf node는 실질적으로 렌더링될 기하요소에 대응되는 노드가 된다. 각 노드는 서브트리를 전체를 포함하는 BV를 가진다. 그리고 당연히 루트 노드는 기하개체 모두를 포함하는 BV를 가진다. BVH를 그림으로 간략히 나타내면 다음과 같다.
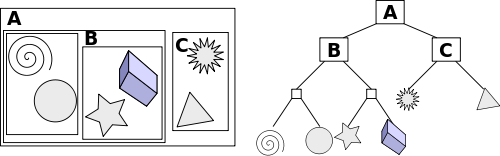
3차원 BVH를 구성할 때, 공간 분할을 가장 긴 축 2개만 이용하면 생성 속도를 좀 더 빠르게 할 수 있다.
예를 들어 씬에 광선을 쏘아서 기하개체랑 교차하는지 여부를 검사해본다고 하자. 가장 먼저 root 노드에 해당되는 BV와 만나는지 검사하고 만나지 않는다면 광선은 기하개체와 아예 교차하지 않는다는 것을 바로 알 수 있다. 반대로 만난다면, 자식노드와의 교차여부를 재귀적으로 검사하면 된다. 광선이 어떤 BV와 만나지 않는 순간, 그 BV에 해당되는 서브트리는 검사를 건너뛰면 된다. 광선이 leaf 노드의 BV와 만난다면 그 곳에 있는 기하개체(예를 들면 삼각형)와 교차점을 정확히 계산하면 된다.
BVH를 구성한 기하개체가 움직이고 있을 때에도 BVH는 유용하다. 어떤 BV에 포함된 오브젝트(예를 들면 삼각형)가 움직였을 때, 해당 BV를 재계산하고, 여전히 부모 BV에 포함되있는지 검사해본다. 만약 포함된다면 BVH는 그대로 유용하고, 그렇지 않다면 해당 오브젝트 노드는 삭제하고 부모 BV는 다시 계산해야한다. 그리고 해당 재계산 했던 BV 노드를 BVH root부터 시작하여 다시 삽입해야 한다.
[참고] Real-time rendering. Akenine-Moller, Tomas, Eric Haines, and Naty Hoffman.
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 메쉬 위의 측지 극좌표 (Geodesic Polar Coordinates on Polygonal Meshes) (0) | 2022.05.04 |
|---|---|
| 직선과 다각형의 교차점 구하기 (0) | 2022.03.16 |
| 삼각형과 박스의 교차여부 구하기 (0) | 2022.03.14 |
| SAT(Separating Axis Test) (0) | 2022.03.14 |
| 세 평면의 교차점 구하기 (0) | 2022.01.27 |



