| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 컴퓨터 구조
- OpenGL
- 오픈지엘
- 셰이더프로그래밍
- Graphics
- 셰이더
- Geometry Modeling
- 윈도우프로그래밍
- MFC 윈도우 프로그래밍
- win32
- c4d
- MFC
- bezier curve
- 윈도우 프로그래밍
- Mesh Processing
- 그래픽스기초
- shader programming
- 윈도우 구조
- 컴퓨터 아키텍쳐
- modeling
- 베지에 곡선
- 렌더링
- 운영체제
- window programming
- shader
- 핵심 API로 배우는 윈도우프로그래밍
- 그래픽스
- denoising
- 윈도우
- Win32 API
- Today
- Total
오다기리 박의 알고리즘 노트
평면과 박스의 교차 검사하기 본문
아래 그림과 같이 3차원 공간에서 평관과 박스의 교차 여부를 검사해보자.
박스의 모든 점들을 평면의 방정식에 대입하여 모든 sigend distance값이 같은 부호라면 교차하지 않고, 부호가 다른값이 나왔다면 정점들이 평면의 양쪽에 존재하므로 둘은 교차하게 된다. 여기서는 AABB와 OBB 각각 다른 방식을 소개한다. 두 방식 모두 박스의 두 점만 평면의 방정식에 대입해보면 된다. 여기서 박스의 두 점은 박스의 중심을 지나는 4개의 대각선들 중 평면의 법선과의 내적값이 가장 큰 대각선의 두 점을 말한다.
우선 박스 B에서 양 끝점, 대각선의 half 벡터, 중심점을 다음과 같이 나타낸다.

half 벡터 h는 박스에서 양 끝점을 어떻게 잡느냐에 따라 총 8개를 구할 수 있다.
이제 다음 그림처럼 3차원 공간에 박스 B와 평면이 놓여 있을 때 의 교차 여부를 판단한다.

다음 e값을 계산함으로써 박스의 half벡터를 평면의 단위 법선에 투영했을 때 가장 큰 길이를 쉽게 얻을 수 있다. 여기서 AABB와 OBB의 계산법이 다르다.
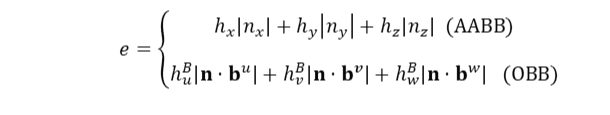
그리고 다음과 같이 박스의 중심점을 평면의 방정식에 대입하여 박스의 중심점에서 평면까지의 signed distance s를 계산한다.
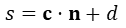
마지막으로, s와 e를 비교하여 박스가 평면의 위쪽에 위치 하는지, 아래쪽에 위치하는지, 교차하는지 여부를 판단한다.
- s - e > 0 이라면 박스는 평면의 위쪽에 위치한다.
- s + e < 0 이라면 박스는 평면의 아래쪽에 위치한다.
- 그 외의 경우에는 박스와 평면이 교차한다.
[참고] Real-time rendering. Akenine-Moller, Tomas, Eric Haines, and Naty Hoffman.
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 세 평면의 교차점 구하기 (0) | 2022.01.27 |
|---|---|
| AABB(Axis-Aligned Bounding Box)와 OBB(Oriented Bounding Box)에 대하여 (2) | 2022.01.27 |
| 직선과 평면의 교차점 구하기 (0) | 2022.01.27 |
| 삼각형 내부점의 무게중심 좌표(barycentric coordinate) 구하기 (3) | 2022.01.26 |
| 네개의 3차원 벡터로 이루어진 행렬 (0) | 2022.01.26 |




