| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- OpenGL
- 셰이더
- 윈도우 구조
- 그래픽스
- modeling
- 오픈지엘
- 윈도우
- shader programming
- 윈도우프로그래밍
- 운영체제
- shader
- denoising
- c4d
- 베지에 곡선
- window programming
- Mesh Processing
- MFC 윈도우 프로그래밍
- Win32 API
- Geometry Modeling
- 윈도우 프로그래밍
- win32
- bezier curve
- 그래픽스기초
- 셰이더프로그래밍
- 렌더링
- 핵심 API로 배우는 윈도우프로그래밍
- 컴퓨터 구조
- Graphics
- 컴퓨터 아키텍쳐
- MFC
- Today
- Total
오다기리 박의 알고리즘 노트
세 평면의 교차점 구하기 본문
3차원 공간에서 다음 방정식으로 표현되는 세 평면의 교차점을 구해보자. 여기서는 4가지 방법을 소개한다.
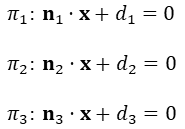
우선 예외처리를 위해 세 평면의 법선이 모두 한 평면위에 있는 경우는 제외한다. 즉 다음 그림처럼 두개 이상의 평면이 평행하거나, 세 평면이 한 직선을 공유하거나, 직선을 공유하지 않는 경우이다.
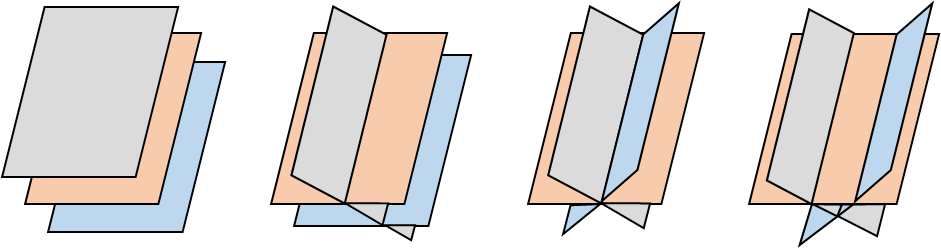
이를 조사하기 위해서는 세 평면의 법선으로 이루어진 행렬의 행렬식이 0인지 조사하면 된다. 행렬식이 0이라면 세 벡터로 이루어진 평행육면체의 부피가 0이므로 세 법선이 한 평면위에 존재하게 된다.
그 외의 경우에는 다음 그림처럼 세 평면이 하나의 유일한 점에서 교차한다.
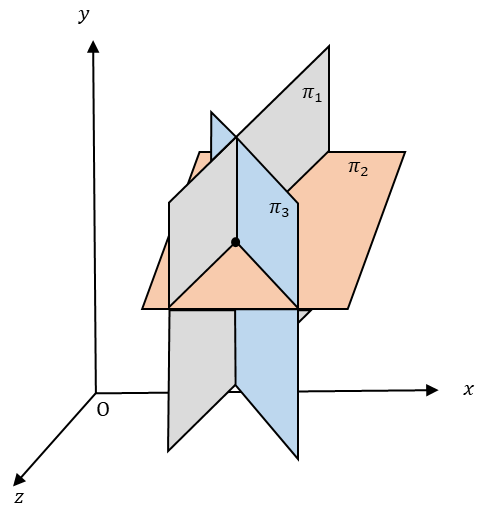
첫번째 방식
첫번째 방식은 다음과 같이 교점 p를 세 평면의 방정식에 각각 대입하여 3개의 연립 방정식을 세운다.
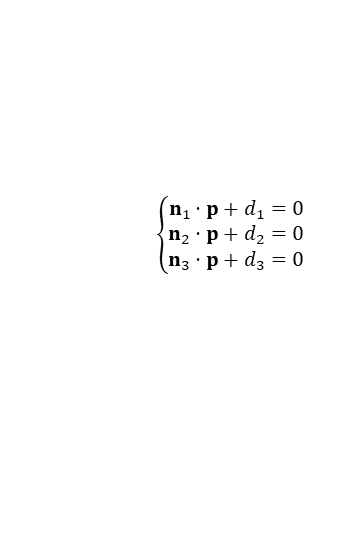
결론적으로 다음 선형 시스템을 풀어서 미지수 p를 구하면 된다. 선형 시스템을 푸는 방법은 LU분해를 이용하여 풀거나 양변을 3x3 역행렬로 나누거나, 크래머 공식을 적용할 수도 있다.
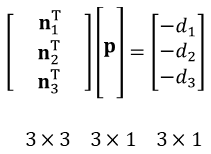
두번째 방식
두번째 방식은 다음 공식을 이용하여 세 평면의 교점 p를 구한다.
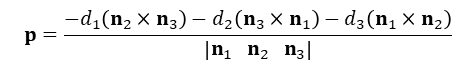
세번째 방식
세번째 방식은 4x4 행렬식을 계산할 때 여인수 전개 (cofactor expansion)를 하는 것과 비슷하다. 다음 식을 계산하면 4차원 homogeneous 좌표 x가 얻어지는데, 각 성분을 4번째 성분으로 나누면 p를 구할 수 있다.
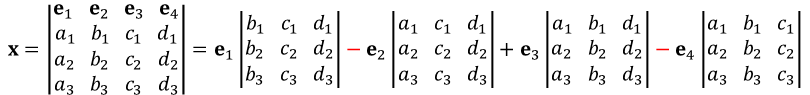
여기서 a, b, c, d 는 평면의 계수를 나타내며 e1=(1, 0, 0, 0), e2=(0, 1, 0, 0), e3=(0, 0, 1, 0), e4=(0, 0, 0, 1)이다. 계산시 마이너스 부호에 주의하자. 만약에 마이너스 부호를 쓰기 싫다면 다음과 같이 행을 바꿔 써도 된다.

네번째 방식
네번째 방식도 세번째와 마찬가지로 4차원 homogeneous 좌표를 구한 뒤 각성분을 4번째 성분으로 나누는 방식인데, 크래머 공식을 응용한다. 이번에는 homogeneous 좌표 x를 다음과 같이 계산한다.
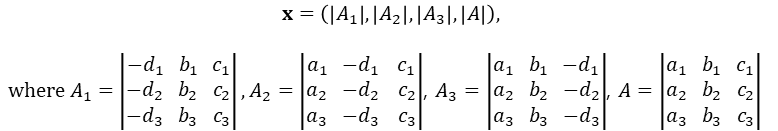
A1, A2, A3의 생김새를 잘 살펴보면, A의 각 열을 (-d1, -d2, -d3)로 대체한 것을 볼 수 있다.
[참고]
Real-time rendering. Akenine-Moller, Tomas, Eric Haines, and Naty Hoffman.
Nehring-Wirxel, Julius, Philip Trettner, and Leif Kobbelt. "Fast exact booleans for iterated CSG using octree-embedded BSPs." Computer-Aided Design 135 (2021)
'컴퓨터 그래픽스 > 메쉬 기하학' 카테고리의 다른 글
| 삼각형과 박스의 교차여부 구하기 (0) | 2022.03.14 |
|---|---|
| SAT(Separating Axis Test) (0) | 2022.03.14 |
| AABB(Axis-Aligned Bounding Box)와 OBB(Oriented Bounding Box)에 대하여 (2) | 2022.01.27 |
| 평면과 박스의 교차 검사하기 (0) | 2022.01.27 |
| 직선과 평면의 교차점 구하기 (0) | 2022.01.27 |



